如图1,在直角梯形ABCD中,AD∥BC,顶点D,C分别在AM,BN上运动(点D不与A重合,点C不与B重合),E是AB上的动点(点E不与A,B重合),在运动过程中始终保持DE⊥CE,且AD+DE=AB=a.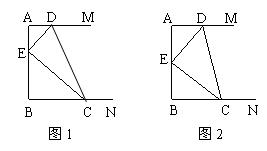
(1)求证:△ADE∽△BEC;
(2)设AE=m,请探究:△BEC的周长是否与m值有关,若有关请用含m的代数式表示△BEC的周长;若无关请说明理由.
(Ⅰ)
(II)
如图所示,四棱锥 的底面 是边长为 1 的菱形, , 是 的中点, 底面 .
(I) 证明: 平面 平面 ;
(Ⅱ)求平面PAD和平面PBE所成二面角(锐角)的大小.

甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约.甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设每人面试合格的概率都是 , 且面试是否合格互不影响.
求: ( I ) 至少有 1 人面试合格的概率;
( II ) 签约人数 的分布列和数学期望.
(1) 求 的值;
(2) 设 , 求证:
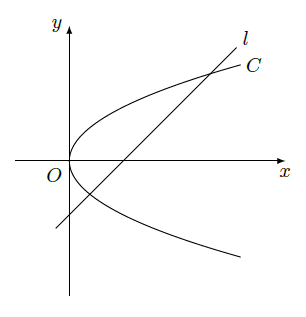
如图, 在平面直角坐标系 中, 已知直线 , 抛物线
(1) 若直线 过抛物线 的焦点, 求抛物线 的方程;
(2) 已知抛物线 上存在关于直线 对称的相异两点 和 .
①求证:线段 的中点坐标为 ;
②求 的取值范围.