已知函数 .设命题p:“
.设命题p:“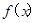 的定义域为R”;命题q:“
的定义域为R”;命题q:“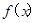 的值域为R”
的值域为R”
(1)分别求命题p、q为真时,实数a的取值范围;
(2)¬p是q的什么条件?请说明理由.
(本小题满分16分)数列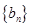
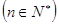 是递增的等比数列,且
是递增的等比数列,且 .
.
(1)求数列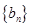 的通项公式;
的通项公式;
(2)若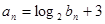 ,求证数列
,求证数列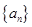 是等差数列;
是等差数列;
(3)若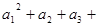 ……
…… ,求
,求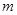 的最大值.
的最大值.
(本小题满分14分).
求倾斜角是直线y=-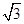 x+1的倾斜角的
x+1的倾斜角的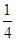 ,且分别满足下列条件的直线方程:
,且分别满足下列条件的直线方程:
(1)经过点(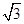 ,-1);
,-1);
(2)在y轴上的截距是-5.
(本小题满分14分)
等差数列{an}不是常数列,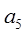 =10,且
=10,且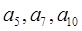 是等比数列{
是等比数列{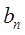 }的第1,3,5项,且
}的第1,3,5项,且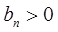 .
.
(1)求数列{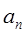 }的第20项,(2)求数列{
}的第20项,(2)求数列{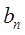 }的通项公式.
}的通项公式.
(本小题满分14分)
已知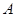 、
、 、
、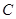 为
为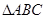 的三内角,且其对边分别为
的三内角,且其对边分别为 、
、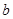 、
、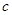 ,若
,若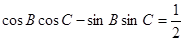 .
.
(1)求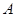 ; (2)若
; (2)若 ,求
,求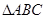 的面积.
的面积.
(本小题满分12分)
已知等差数列 中,
中,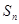 是其前
是其前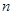 项和,
项和,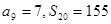 ,求:
,求: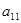 及
及 .
.