已知函数 ,设命题
,设命题 :“
:“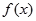 的定义域为
的定义域为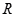 ”;
”;
命题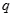 :“
:“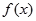 的值域为
的值域为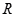 ” .
” .
(1)分别求命题 、
、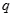 为真时实数
为真时实数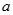 的取值范围;
的取值范围;
(2)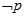 是
是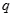 的什么条件?请说明理由.
的什么条件?请说明理由.
(本小题满分14分)
设函数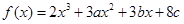 在
在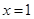 及
及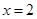 时取得极值.
时取得极值.
(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的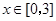 ,都有
,都有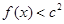 成立,求c的取值范围。
成立,求c的取值范围。
(本小题满分12分)
已知椭圆C: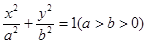 ,它的离心率为
,它的离心率为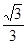 .直线
.直线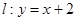 与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程.
与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程.
(本小题满分12分)
已知 关于
关于 的方程
的方程 有两个不等的负根;
有两个不等的负根; 关于
关于 的方程
的方程 无实根。若
无实根。若 为真,
为真, 为假,求
为假,求 的取值范围
的取值范围
(本小题满分14分)
已知等差数列{an}的首项为a,公差为b,等比数列{bn}的首项为b,公比为a,存在m,n∈N+使得am+1=bn成立,其中a,b均为正整数,且a1<b1<a2<b2<a3 ;
(1)求数列{an},{bn}的通项公式;
(2)设函数f(x)=bmx+bm-1x2+…+b1xm,f′(x)是函数f(x)的导函数;令Sm=f′(1),求Sm(用含n的代数式表示)
(本小题满分13分)
如图M为的△ABC的中线AD的中点,过M的直线分别与边AB,AC交于点P,Q,设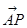 =x
=x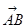 ,
,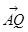 =y
=y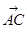 ,记y=f(x)
,记y=f(x)
(1)求函数y=f(x)的表达式;
(2)设g(x)=x3+3a2x+2a,(x∈[0,1]),若对于任意x1∈[ ,1],总存在x2∈[0,1]使得f(x1)=g(x2)成立,求实数a的取值范围;
,1],总存在x2∈[0,1]使得f(x1)=g(x2)成立,求实数a的取值范围;