设 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数 的最小值为-12.
的最小值为-12.
(1)求 的值;
的值;
(2)求函数 的单调递增区间,极大值和极小值,并求函数f(x)在
的单调递增区间,极大值和极小值,并求函数f(x)在 上的最大值与最小值.
上的最大值与最小值.
设函数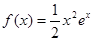 .
.
(1)求f(x)的单调区间;
(2)若当x∈[-2,2]时,不等式f(x)>m恒成立,求实数m的取值范围
已知直线 与双曲线
与双曲线 ;
;
(1)当a为何值时,直线与双曲线有一个交点;
(2)直线与双曲线交于P、Q两点且以PQ为直径的圆过坐标原点,求a值。
(本小题满分14分)
如图,椭圆
 的顶点为
的顶点为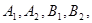 焦点为
焦点为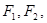
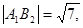 S□
S□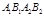 = 2S□
= 2S□ .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线 过P(1,1),且与椭圆相交于A,B两点,当P是AB的中点时,求直线
过P(1,1),且与椭圆相交于A,B两点,当P是AB的中点时,求直线 的方程.
的方程.
(Ⅲ)设n为过原点的直线, 是与n垂直相交于P点、与
是与n垂直相交于P点、与
椭圆相交于A,B两点的直线,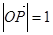 ,是否存在上述直线
,是否存在上述直线 使以AB为直径的圆过原点?若存在,求出直线
使以AB为直径的圆过原点?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分12分)
如图,已知直线 与抛物线
与抛物线 相交于
相交于 两点,与
两点,与 轴相交于点
轴相交于点 ,若
,若 .
.
(Ⅰ)求证: 点的坐标为(1,0);
点的坐标为(1,0);
(Ⅱ)求△AOB的面积的最小值.
(本小题满分12分)
给定两个命题, :对任意实数
:对任意实数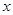 都有
都有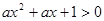 恒成立;
恒成立;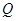 :关于
:关于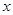 的方程
的方程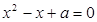 有实数根.如果
有实数根.如果 ∨
∨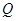 为真命题,
为真命题, ∧
∧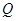 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.