(1)设 ,求证:
,求证: 
(2)已知正数x、y满足2x+y=1,求 的最小值及对应的x、y值.
的最小值及对应的x、y值.
(3)已知实数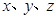 满足
满足 ,
,  的最大值及对应的x、y、z值.
的最大值及对应的x、y、z值.
(本小题满分14分)设函数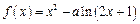 (
( ,
,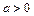 ).
).
(1)若函数 在其定义域内是减函数,求
在其定义域内是减函数,求 的取值范围;
的取值范围;
(2)函数 是否有最小值?若有最小值,指出其取得最小值时
是否有最小值?若有最小值,指出其取得最小值时 的值,并证明你的结论.
的值,并证明你的结论.
(本题14分)用长度为18cm的钢条围成一个长方体形状的框架,要求长方体的长和宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积为多少?
(本题14分)已知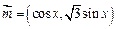 ,
, ,设
,设 .
.
(1)求函数 的图像的对称轴及其单调递增区间;
的图像的对称轴及其单调递增区间;
(2)当 ,求函数
,求函数 的值域及取得最大值时
的值域及取得最大值时 的值;
的值;
(3)若 分别是锐角
分别是锐角 的内角
的内角 的对边,且
的对边,且 ,
,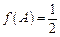 ,试求
,试求 的面积
的面积 .
.
(本题14分)已知函数
(1)讨论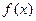 的单调区间;
的单调区间;
(2)若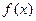 在
在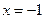 处取得极值,直线y=m与
处取得极值,直线y=m与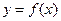 的图象有三个不同的交点,求m的取值范围。
的图象有三个不同的交点,求m的取值范围。
(本题12分)函数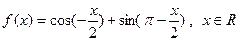 。
。
(1)求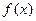 的最小正周期;
的最小正周期;
(2)若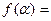
 ,
,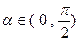 ,求
,求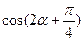 的值。
的值。