已知函数 在
在 与
与 时都取得极值.
时都取得极值.
(1)求 的值;
的值;
(2)若对 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
如图①,在等腰直角三角形
中,
,
,
分别是
上的点,
,
为
的中点.将
沿
折起,得到如图②所示的四棱锥
,其中
.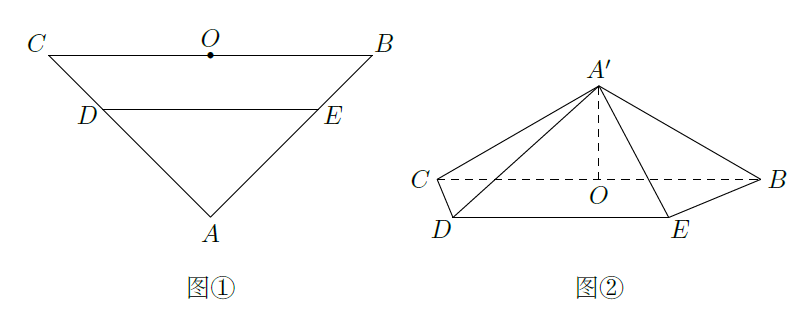
(Ⅰ) 证明:
;
(Ⅱ) 求二面角
的平面角的余弦值.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.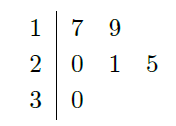
(Ⅰ) 根据茎叶图计算样本均值;
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人;
(Ⅲ) 从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.
已知函数
.
(Ⅰ) 求
的值;
(Ⅱ) 若
,求
.
设F为抛物线E: 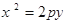
 的焦点,A、B、C为该抛物线上三点,已知
的焦点,A、B、C为该抛物线上三点,已知 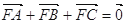 且
且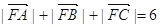 .
.
(1)求抛物线方程;
(2)设动直线l与抛物线E相切于点P,与直线 相交于点Q。证明以PQ为直径的圆恒过y轴上某定点。
相交于点Q。证明以PQ为直径的圆恒过y轴上某定点。
某商区停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过 小时收费
小时收费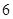 元,超过
元,超过 小时的部分每小时收费
小时的部分每小时收费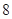 元(不足
元(不足 小时的部分按
小时的部分按 小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过
小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过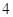 小时.
小时.
(1)若甲停车 小时以上且不超过
小时以上且不超过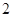 小时的概率为
小时的概率为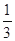 ,停车付费多于
,停车付费多于 元的概率为
元的概率为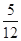 ,求甲停车付费恰为
,求甲停车付费恰为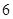 元的概率;
元的概率;
(2)若每人停车的时长在每个时段的可能性相同,求甲、乙二人停车付费之和为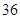 元的概率.
元的概率.