已知函数
 .
.
(1)求函数 的极值;
的极值;
(2)证明:当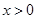 时,
时,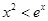 ;
;
(3)证明:对任意给定的正数 ,总存在
,总存在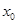 ,使得当
,使得当 ,恒有
,恒有 .
.
如图,三棱柱 中,
中, ,
,  ,平面
,平面 平面
平面 ,
, 与
与 相交于点
相交于点 .
.
(1)求证: 平面
平面 ;
;
(2)设点 是直线
是直线 上一点,且
上一点,且 平面
平面 ,求平面
,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.
南昌三中高三年级举行投篮比赛,比赛规则如下:每次投篮投中一次得 分,未中扣
分,未中扣 分,每位同学原始积分均为
分,每位同学原始积分均为 分,当累积得分少于或等于
分,当累积得分少于或等于 分则停止投篮,否则继续,每位同学最多投篮
分则停止投篮,否则继续,每位同学最多投篮 次.且规定总共投中
次.且规定总共投中 次的同学分别为一、二、三等奖,奖金分别为
次的同学分别为一、二、三等奖,奖金分别为 元、
元、 元、
元、 元.某班甲、乙、丙同学相约参加此活动,他们每次投篮命中的概率均为
元.某班甲、乙、丙同学相约参加此活动,他们每次投篮命中的概率均为 ,且互不影响.
,且互不影响.
(1)求甲同学能获奖的概率;
(2)记甲、乙、丙三位同学获得奖金总数为 ,求
,求 的期望
的期望 .
.
已知 的面积
的面积 满足
满足 ,且
,且 .
.
(Ⅰ)求角 的取值范围;
的取值范围;
(Ⅱ)若函数 ,求
,求 的最大值.
的最大值.
已知数列{an}的首项a1=a,Sn是数列{an}的前n项和,且满足: =3n2an+
=3n2an+ ,an≠0,n≥2,n∈N*.
,an≠0,n≥2,n∈N*.
(1)若数列{an}是等差数列,求a的值;
(2)确定a的取值集合M,使a∈M时,数列{an}是递增数列.
(本题满分16分)
设函数 .
.
(1)若 =1时,函数
=1时,函数 取最小值,求实数
取最小值,求实数 的值;
的值;
(2)若函数 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数 的取值范围;
的取值范围;
(3)若 ,证明对任意正整数
,证明对任意正整数 ,不等式
,不等式 都成立.
都成立.