设 =
= ,其中
,其中 为正实数.
为正实数.
(1)当
 时,求
时,求 的极值点;
的极值点;
(2)若 为
为 上的单调函数,求
上的单调函数,求 的取值范围。
的取值范围。
已知矩形 中,
中,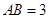 ,
,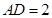 ,点
,点 在
在 上且
上且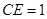 (如图(3)).把
(如图(3)).把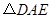 沿
沿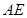 向上折起到
向上折起到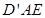 的位置,使二面角
的位置,使二面角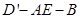 的大小为
的大小为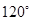 (如图(4)).
(如图(4)).
(Ⅰ)求四棱锥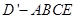 的体积;
的体积;
(Ⅱ)求 与平面
与平面 所成角的正切值;
所成角的正切值;
(Ⅲ)设 为
为 的中点,是否存在棱
的中点,是否存在棱 上的点
上的点 ,使
,使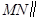 平面
平面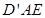 ?若存在,试求出
?若存在,试求出 点位置;若不存在,请说明理由.
点位置;若不存在,请说明理由.
设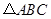 的内角
的内角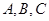 所对的边长分别为
所对的边长分别为 ,且
,且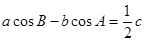 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的最大值,并判断当
的最大值,并判断当 取最大值时
取最大值时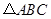 的形状.
的形状.
2011年3月20日,第19个世界水日,主题是:“城市水资源管理”;2011年“六·五”世界环境日中国主题:“共建生态文明,共享绿色未来”.活动组织者为调查市民对活动主题的了解情况,随机对10~60岁的人群抽查了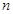 人,调查的每个人都同时回答了两个问题,统计结果如下:
人,调查的每个人都同时回答了两个问题,统计结果如下: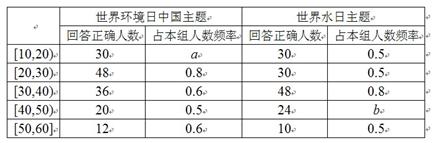
(Ⅰ)若以表中的频率近似看作各年龄段回答活动主题正确的概率,规定回答正确世界环境日中国主题的得20元奖励,回答正确世界水日主题的得30元奖励.组织者随机请一个家庭中的两名成员(大人42岁,孩子16岁)回答这两个主题,两个主题能否回答正确均无影响,分别写出这个家庭两个成员获得奖励的分布列并求该家庭获得奖励的期望;
(Ⅱ)求该家庭获得奖励为50元的概率.
已知函数 ,
,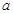 为实数.
为实数.
(Ⅰ)当 时,求函数
时,求函数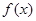 的单调增区间;
的单调增区间;
(Ⅱ)若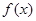 在闭区间
在闭区间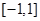 上为减函数,求
上为减函数,求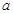 的取值范围.
的取值范围.
设函数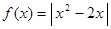 .
.
(1)在区间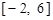 上画出函数
上画出函数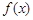 的图象;
的图象;
(2)根据图象写出该函数在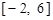 上的单调增区间;
上的单调增区间;
(3)方程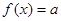 在区间
在区间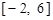 有两个不同的实数根,求
有两个不同的实数根,求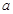 的取值范围.
的取值范围.