某年级先后举办了数学、历史、音乐的讲座,其中有75人听了数学讲座,68人听了历史讲座,61人听了音乐讲座,17人同时听了数学、历史讲座,12人同时听了数学、音乐讲座,9人同时听了历史、音乐讲座,还有6人听了全部讲座.求听讲座的人数.
已知直角 的三边长
的三边长 ,满足
,满足
(1)在 之间插入2011个数,使这2013个数构成以
之间插入2011个数,使这2013个数构成以 为首项的等差数列
为首项的等差数列 ,且它们的和为
,且它们的和为 ,求的最小值;
,求的最小值;
(2)已知 均为正整数,且
均为正整数,且 成等差数列,将满足条件的三角形的面积从小到大排成一列
成等差数列,将满足条件的三角形的面积从小到大排成一列 ,且
,且 ,求满足不等式
,求满足不等式 的所有
的所有 的值;
的值;
(3)已知 成等比数列,若数列
成等比数列,若数列 满足
满足 ,证明:数列
,证明:数列 中的任意连续三项为边长均可以构成直角三角形,且
中的任意连续三项为边长均可以构成直角三角形,且 是正整数.
是正整数.
设函数
(1)当  ,画出函数
,画出函数 的图像,并求出函数
的图像,并求出函数 的零点;
的零点;
(2)设 ,且对任意
,且对任意 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知向量 向量
向量 与向量
与向量 的夹角为
的夹角为 ,且
,且 。
。
(1 )求向量 ;
;
(2)若向量 与
与 共线,向量
共线,向量 ,其中
,其中 、
、 为
为 的内角,且
的内角,且 、
、 、
、 依次成等差数列,求
依次成等差数列,求 的取值范围.
的取值范围.
本题共有2个小题,第(1)小题满分6分,第(2)小题满分6分.
如图,已知正四棱柱 的底面边长是
的底面边长是 ,体积是
,体积是 ,
, 分别是棱
分别是棱 、
、 的中点.
的中点.
(1)求直线 与平面
与平面 所成的角(结果用反三角函数表示);
所成的角(结果用反三角函数表示);
(2)求过 的平面与该正四棱柱所截得的多面体
的平面与该正四棱柱所截得的多面体 的体积.
的体积.
已知数集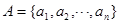 ,其中
,其中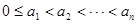 ,且
,且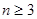 ,若对
,若对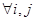 (
( ),
), 与
与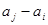 两数中至少有一个属于
两数中至少有一个属于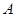 ,则称数集
,则称数集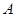 具有性质
具有性质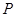 .
.
(Ⅰ)分别判断数集 与数集
与数集 是否具有性质
是否具有性质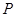 ,说明理由;
,说明理由;
(Ⅱ)已知数集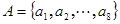 具有性质
具有性质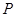 ,判断数列
,判断数列 是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
是否为等差数列,若是等差数列,请证明;若不是,请说明理由.