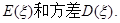已知椭圆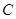 的中心在原点,焦点在
的中心在原点,焦点在 轴上,且过点
轴上,且过点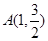 和
和 .
.
(1)求椭圆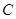 的方程;
的方程;
(2)若椭圆 与椭圆
与椭圆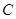 有相同的焦点,且过点
有相同的焦点,且过点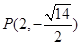 ,求椭圆
,求椭圆 的方程.
的方程.
已知函数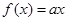 ,
, ,其中
,其中
(Ⅰ)若函数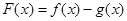 有极值
有极值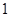 ,求实数
,求实数 的值;
的值;
(Ⅱ)若函数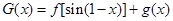 在区间
在区间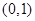 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(Ⅲ)证明: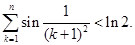
已知抛物线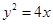 的焦点为
的焦点为 ,点
,点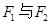 关于坐标原点对称,以
关于坐标原点对称,以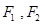 为焦点的椭圆
为焦点的椭圆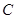 ,过点
,过点
(Ⅰ)求椭圆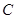 的标准方程;
的标准方程;
(Ⅱ)设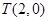 ,过点
,过点 作直线
作直线 与椭圆
与椭圆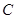 交于
交于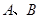 两点,且
两点,且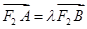 ,若
,若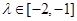 ,求
,求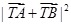 的最小值。
的最小值。
香港违法“占中”行动对香港的经济、政治、社会及民生造成重大损失,据香港科技大学经济系教授雷鼎鸣测算,仅香港的“占中”行动开始后一个多月的时间,保守估计造成经济损失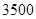 亿港元,相等于平均每名港人承受了
亿港元,相等于平均每名港人承受了 万港元的损失,为了挽回经济损失,某厂家拟在新年举行大型的促销活动,经测算某产品当促销费用为
万港元的损失,为了挽回经济损失,某厂家拟在新年举行大型的促销活动,经测算某产品当促销费用为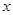 万元时,销售量
万元时,销售量 万件满足
万件满足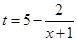 (其中
(其中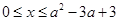 ,
,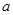 为正常数).现假定生产量与销售量相等,已知生产该产品
为正常数).现假定生产量与销售量相等,已知生产该产品 万件还需投入成本
万件还需投入成本 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为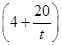 万元/万件.
万元/万件.
(1)将该产品的利润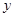 万元表示为促销费用
万元表示为促销费用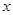 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
若数列 满足
满足 ,则称数列
,则称数列 为“平方递推数列”.已知数列
为“平方递推数列”.已知数列 中,
中, ,点
,点 在函数
在函数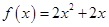 的图象上,其中
的图象上,其中 为正整数.
为正整数.
(1)证明数列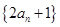 是“平方递推数列”,且数列
是“平方递推数列”,且数列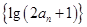 为等比数列;
为等比数列;
(2)设(1)中“平方递推数列”的前 项之积为
项之积为 ,即
,即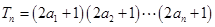 ,求数列
,求数列 的通项及
的通项及 关于
关于 的表达式;
的表达式;
(3)记 ,求数列
,求数列 的前
的前 项和
项和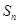 ,并求使
,并求使 的
的 的最小值.
的最小值.
某居民小区有两个相互独立的安全防范系统(简称系统)甲和乙,系统甲和系统乙在任意时刻发生故障的概率分别为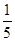 和
和 ,若在任意时刻至多有一个系统发生故障的概率为
,若在任意时刻至多有一个系统发生故障的概率为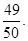
(Ⅰ)求 的值;
的值;
(Ⅱ)设系统乙在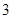 次相互独立的检测中不发生故障的次数为随机变量
次相互独立的检测中不发生故障的次数为随机变量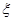 ,求
,求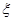 的数学期望
的数学期望