(本题共12分)设函数 ,若对
,若对 均有
均有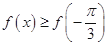 恒成立.
恒成立.
(Ⅰ)求实数 的值及函数
的值及函数 的单调递减区间;
的单调递减区间;
(Ⅱ)在 中,
中,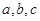 分别为内角
分别为内角 所对的边,且
所对的边,且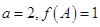 ,求
,求 的内切圆半径
的内切圆半径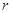 的最大值.
的最大值.
已知以原点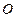 为中心的双曲线的一条准线方程为
为中心的双曲线的一条准线方程为 ,离心率
,离心率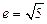 .
.
(Ⅰ)求该双曲线的方程;
(Ⅱ)如图,点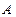 的坐标为
的坐标为 ,
,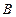 是圆
是圆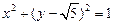 上的点,点
上的点,点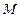 在双曲线右支上,求
在双曲线右支上,求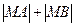 的最小值,并求此时
的最小值,并求此时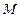 点的坐标;
点的坐标;


(Ⅰ)当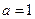 时,证明函数
时,证明函数 只有一个零点;
只有一个零点;
(Ⅱ)若函数 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的取值范围
的取值范围
(1)求证: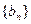 是等差数列;
是等差数列;
(2)求数列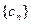 的前n项和Sn;
的前n项和Sn;
(3)若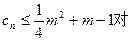 一切正整数n恒成立,求实数m的取值范围
一切正整数n恒成立,求实数m的取值范围
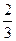
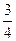
(1)设 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求 的分布列及
的分布列及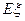 ;
;
(2)设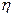 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数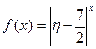 在定义域内单调递减”为事件
在定义域内单调递减”为事件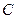 ,求事件
,求事件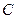 的概率
的概率

侧棱PA=PD= ,底面ABCD为直角梯形,其中
,底面ABCD为直角梯形,其中
BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(1)求证:PO⊥平面ABCD;
(2)求异面直线PB与CD所成角的余弦值;
(3)线段AD上是否存在点Q,使得它到平面PCD的距离为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.