(本小题满分为12分)某种商品原来每件售价为25元,年销售8万件.
(Ⅰ)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(Ⅱ)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到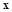 元.公司拟投入
元.公司拟投入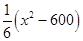 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量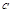 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率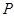 与日产量
与日产量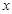 (件)(
(件)(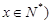 之间大体满足如框图所示的关系(注:次品率
之间大体满足如框图所示的关系(注:次品率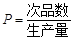 ).又已知每生产一件合格的仪器可以盈利
).又已知每生产一件合格的仪器可以盈利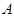 (元),但每生产一件次品将亏损
(元),但每生产一件次品将亏损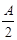 (元).(其中c为小于96的常数)
(元).(其中c为小于96的常数)
(1)若c=50,当x="46" 时,求次品率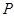 ;
;
(2)求日盈利额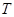 (元)与日产量
(元)与日产量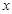 (件)(
(件)(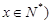 的函数关系;
的函数关系;
(3)当日产量为多少时,可获得最大利润?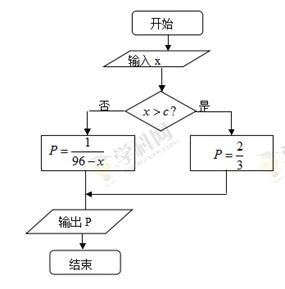
已知数列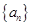 的前三项分别为
的前三项分别为 ,
, ,
,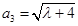 ,(其中
,(其中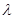 为正常数)。设
为正常数)。设
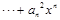 。
。
(1)归纳出数列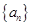 的通项公式,并证明数列
的通项公式,并证明数列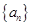 不可能为等比数列;
不可能为等比数列;
(2)若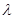 =1,求
=1,求 的值;
的值;
(3)若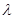 =4,试证明:当
=4,试证明:当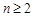 时,
时, .
.
我校为了了解高二级学生参加体育活动的情况,随机抽取了100名高二级学生进行调查.下面是根据调查结果绘制的学生日均参加体育活动时间的频率分布直方图: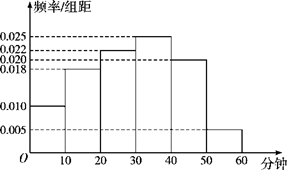
将日均参加体育活动时间不低于40分钟的学生称为参加体育活动的“积极分子”.根据已知条件完成下面的列联表,并据此资料,在犯错误的概率不超过5%的前提下,你是否认为参加体育活动的“积极分子”与性别有关?
| 非积极分子 |
积极分子 |
合计 |
|
| 男 |
15 |
45 |
|
| 女 |
|||
| 合计 |
某种产品的广告费支出x与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
50 |
60 |
70 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 .
.
(3)经计算,相关指数 ,你可得到什么结论?
,你可得到什么结论?
(参考数值:2×30+4×40+5×50+6×60+8×70==1390)
在直角坐标系xOy中,直线l的方程为x-y+2=0,
曲线C的参数方程为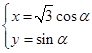 (α为参数).
(α为参数).
(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为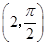 ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线l的距离的最大值.