(本小题满分14分)设函数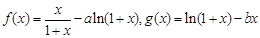 .
.
(1)若函数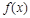 在
在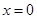 处有极值,求函数
处有极值,求函数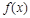 的最大值;
的最大值;
(2)①是否存在实数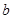 ,使得关于
,使得关于 的不等式
的不等式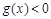 在
在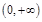 上恒成立?若存在,求出
上恒成立?若存在,求出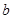 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
②证明:不等式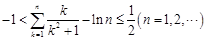 .
.
(本小题满分10分)如图, 的半径
的半径 垂直于直径
垂直于直径 ,
, 为
为 上一点,
上一点, 的延长线交
的延长线交 于
于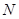 ,过
,过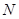 点的切线交
点的切线交 的延长线于
的延长线于 。
。
(1)求证: ;
;
(2)若 的半径为
的半径为 ,
, .求:
.求: 的长。
的长。
(本小题满分12分) 已知函数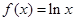 .
.
(1)求函数 的最大值;
的最大值;
(2)求证:
(3)当 时,求证:
时,求证: .
.
(本小题满分12分)过椭圆 的右焦点
的右焦点 作斜率
作斜率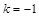 的直线交椭圆于
的直线交椭圆于 两点,且
两点,且 与
与 共线.
共线.
(1)求椭圆的离心率;
(2)设 为椭圆上任意一点,且
为椭圆上任意一点,且 ,证明:
,证明: 为定值。
为定值。
(本小题满分12分)如图,正方形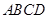 所在平面与等腰三角形
所在平面与等腰三角形 所在平面相交于
所在平面相交于
 平面
平面 .
.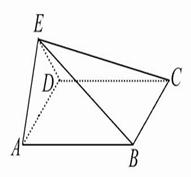
(1)求证: 平面
平面 ;
;
(2)设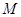 是线段
是线段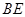 上一点,当直线
上一点,当直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 时,试确定点
时,试确定点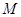 的位置.
的位置.
(本小题满分12分)为了促进学生的全面发展,贵州某中学重视学生社团文化建设,2014年该校某新生确定争取进入曾获团中央表彰的“海济社”和“话剧社”。已知该同学通过考核选拨进入两个社团成功与否相互独立,根据报名情况和他本人的才艺能力,两个社团都能进入的概率为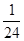 ,至少进入一个社团的概率为
,至少进入一个社团的概率为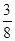 ,并且进入“海济社”的概率小于进入“话剧社”的概率。
,并且进入“海济社”的概率小于进入“话剧社”的概率。
(1)求该同学分别通过选拨进入“海济社”的概率 和进入“话剧社”的概率
和进入“话剧社”的概率 ;
;
(2)学校根据这两个社团的活动安排情况,对进入“海济社”的同学增加1个校本选修课学分,对进入“话剧社”的同学增加0.5个校本选修课学分.求该同学在社团方面获得校本选修加分分数的分布列和数学期望。