(本小题满分12分)某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如下图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
(1)问各班被抽取的学生人数各为多少人?
(2)求平均成绩.
(3)在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率.
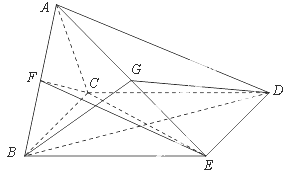
如图,四棱锥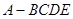 中,
中, 是正三角形,四边形
是正三角形,四边形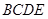 是矩形,且平面
是矩形,且平面 平面
平面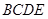 ,
, ,
, .
.
(Ⅰ)若点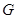 是
是 的中点,求证:
的中点,求证: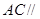 平面
平面 ;
;
(II)试问点 在线段
在线段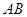 上什么位置时,二面角
上什么位置时,二面角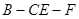 的余弦值为
的余弦值为 .
.
已知定点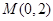 ,
,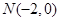 ,直线
,直线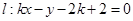 (
( 为常数).
为常数).
(1)若点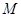 、
、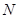 到直线
到直线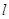 的距离相等,求实数
的距离相等,求实数 的值;
的值;
(2)对于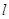 上任意一点
上任意一点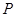 ,
,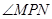 恒为锐角,求实数
恒为锐角,求实数 的取值范围.
的取值范围.
已知向量 ,设函数
,设函数 +1
+1
(1)若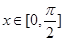 ,
,  ,求
,求 的值;
的值;
(2)在△ABC中,角A,B,C的对边分别是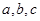 ,且满足
,且满足 ,求
,求
的取值范围.
设集合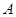 为函数
为函数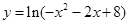 的定义域,集合
的定义域,集合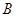 为函数
为函数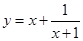 的值域,集合
的值域,集合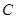 为不等式
为不等式 的解集.
的解集.
(1)求 ;
;
(2)若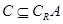 ,求
,求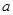 的取值范围.
的取值范围.
如图,已知四边形ABCD内接于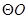 ,且AB是的
,且AB是的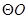 直径,过点D的
直径,过点D的 的切线与BA的延长线交于点M.
的切线与BA的延长线交于点M.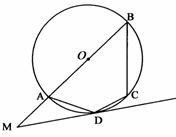
(1)若MD=6,MB=12,求AB的长;
(2)若AM=AD,求∠DCB的大小.