(本小题满分10分）高致病性禽流感是比SARS传染速度更快的-优题课

(本小题满分10分）高致病性禽流感是比SARS传染速度更快的传染病．为防止禽流感蔓延，政府规定：离疫点3km范围内为扑杀区；离疫点3km～5km范围内为免疫区，对扑杀区与免疫区内的村庄、道路实行全封闭管理．现有一条笔直的公路AB通过禽流感病区，如图，在扑杀区内公路CD长为4km．

（1）请用直尺和圆规找出疫点O（不写作法，保留作图痕迹）；
（2）求这条公路在免疫区内有多少千米？

科目数学题型解答题难度中等

知识点：三角形的五心

在等腰 $ΔABC$ 中， $AB = BC$ ，点 $D$ ， $E$ 在射线 $BA$ 上， $BD = DE$ ，过点 $E$ 作 $EF / / BC$ ，交射线 $CA$ 于点 $F$ ．请答案下列问题：

（1）当点 $E$ 在线段 $AB$ 上， $CD$ 是 $ΔACB$ 的角平分线时，如图①，求证： $AE + BC = CF$ ；（提示：延长 $CD$ ， $FE$ 交于点 $M$ ． $)$

（2）当点 $E$ 在线段 $BA$ 的延长线上， $CD$ 是 $ΔACB$ 的角平分线时，如图②；当点 $E$ 在线段 $BA$ 的延长线上， $CD$ 是 $ΔACB$ 的外角平分线时，如图③，请直接写出线段 $AE$ ， $BC$ ， $CF$ 之间的数量关系，不需要证明；

（3）在（1）、（2）的条件下，若 $DE = 2 AE = 6$ ，则 $CF =$ 　　．

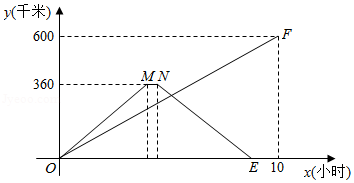
在一条公路上依次有 $A$ ， $B$ ， $C$ 三地，甲车从 $A$ 地出发，驶向 $C$ 地，同时乙车从 $C$ 地出发驶向 $B$ 地，到达 $B$ 地停留0.5小时后，按原路原速返回 $C$ 地，两车匀速行驶，甲车比乙车晚1.5小时到达 $C$ 地．两车距各自出发地的路程 $y$ （千米）与时间 $x$ （小时）之间的函数关系如图所示．请结合图象信息答案下列问题：

（1）甲车行驶速度是　　千米1时， $B$ ， $C$ 两地的路程为　　千米；

（2）求乙车从 $B$ 地返回 $C$ 地的过程中， $y$ （千米）与 $x$ （小时）之间的函数关系式（不需要写出自变量 $x$ 的取值范围）；

（3）出发多少小时，行驶中的两车之间的路程是15千米？请你直接写出答案．

某中学为了了解本校学生对排球、篮球、毽球、羽毛球和跳绳五项“大课间”活动的喜欢情况，随机抽查了部分学生进行问卷调查（每名学生只选择一项），将调查结果整理并绘制成如图所示不完整的统计图表．请结合统计图表答案下列问题：

抽样调查学生喜欢大课间活动人数的统计表

项目	人数
$A$ 排球	6
$B$ 篮球	$m$
$C$ 毽球	10
$D$ 羽毛球	4
$E$ 跳绳	18

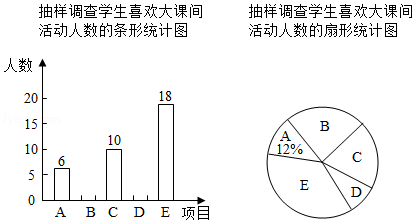
（1）本次抽样调查的学生有　50　人，请补全条形统计图；

（2）求扇形统计图中，喜欢毽球活动的学生人数所对应圆心角的度数；

（3）全校有学生1800人，估计全校喜欢跳绳活动的学生人数是多少？

在 $ΔABC$ 中， $AB = AC$ ， $BC = 6$ ， $S_{ΔABC} = 6$ ．以 $BC$ 为边作周长为18的矩形 $BCDE$ ， $M$ ， $N$ 分别为 $AC$ ， $CD$ 的中点，连接 $MN$ ．请你画出图形，并直接写出线段 $MN$ 的长．

如图，抛物线 $y = x^{2} + bx + c$ 与 $x$ 轴交于 $A$ ， $B$ 两点，与 $y$ 轴交于点 $C$ ，抛物线的顶点为 $P$ ．已知 $B (1, 0)$ ， $C (0, - 3)$ ．请答案下列问题：

（1）求抛物线的解析式，并直接写出点 $P$ 的坐标；

（2）抛物线的对称轴与 $x$ 轴交于点 $E$ ，连接 $AP$ ， $AP$ 的垂直平分线交直线 $PE$ 于点 $M$ ，则线段 $EM$ 的长为　 $\frac{3}{2}$ 　．

注：抛物线 $y = a x^{2} + bx + c (a \neq 0)$ 的对称轴是直线 $x = - \frac{b}{2 a}$ ，顶点坐标是 $(- \frac{b}{2 a}$ ， $\frac{4 ac - b^{2}}{4 a})$ ．