(本小题满分13分)已知平面 平面
平面 ,四边形
,四边形 是矩形,
是矩形,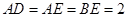 ,
,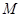 、
、 分别是
分别是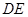 、
、 的中点,主(正)视图方向垂直平面
的中点,主(正)视图方向垂直平面 时,左(侧)视图的面积为
时,左(侧)视图的面积为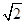 .
.
(1)求证: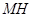 ∥平面
∥平面 ;
;
(2)求证:平面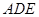
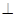 平面
平面 .
.
如图3,正方体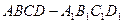 中,
中,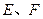 分别为
分别为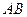
与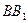 的中点.
的中点.
(Ⅰ)求证: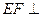 平面
平面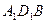 ;
;
(Ⅱ)求二面角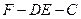 的正切值.
的正切值.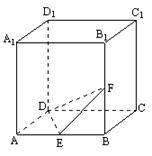
一个多面体的直观图、正(主)视图、侧(左)视图如图1和图2所示,其中正(主)视图、侧(左)视图均为边长为 的正方形.
的正方形.
(Ⅰ)请在图2指定的位置画出多面体的俯视图;
(Ⅱ)若多面体底面对角线AC、BD交于点O,E为线段AA1的中点,求证:OE∥平面A1C1C;
(Ⅲ)求该多面体的表面积.

若三条直线 ,
, ,
, 能围成三角形,求m的取值范围.
能围成三角形,求m的取值范围.
(已知数列 的首项
的首项 (a是常数,且
(a是常数,且 ),
), (
( ),数列
),数列 的首项
的首项 ,
, (
( ).
).
(1)证明: 从第2项起是以2为公比的等比数列;
从第2项起是以2为公比的等比数列;
(2)设 为数列
为数列 的前n项和,且
的前n项和,且 是等比数列,求实数
是等比数列,求实数 的值;
的值;
(3)当a>0时,求数列 的最小项.
的最小项.
(设z=2x+y,变量x,y满足条件
(1)求z的最大值 与最小值
与最小值 ;
;
(2)已知  ,求
,求 的最大值及此时
的最大值及此时 的值;
的值;
(3)已知  ,求
,求 的最小值及此时
的最小值及此时 的值.
的值.