已知函数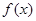 定义在
定义在 上,对于任意的
上,对于任意的 ,有
,有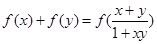 ,且当
,且当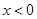 时,
时, .
.
(1)验证函数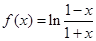 是否满足这些条件;
是否满足这些条件;
(2)若 ,且
,且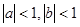 ,求
,求 的值.
的值.
(3)若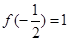 ,试解关于
,试解关于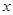 的方程
的方程 .
.
已知函数f(x)=3-2log2x,g(x)=log2x.
(1)如果x∈[1,4],求函数h(x)=(f(x)+1)g(x)的值域;
(2)求函数M(x)=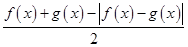 的最大值;
的最大值;
(3)如果不等式f(x2)f(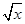 )>kg(x)对x∈[2,4]有解,求实数k的取值范围.
)>kg(x)对x∈[2,4]有解,求实数k的取值范围.
将52名志愿者分成A,B两组参加义务植树活动,A组种植150捆白杨树苗,B组种植200捆沙棘树苗.假定A,B两组同时开始种植.
(1)根据历年统计,每名志愿者种植一捆白杨树苗用时 小时,种植一捆沙棘树苗用时
小时,种植一捆沙棘树苗用时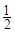 小时.应如何分配A,B两组的人数,使植树活动持续时间最短?
小时.应如何分配A,B两组的人数,使植树活动持续时间最短?
(2)在按(1)分配的人数种植1小时后发现,每名志愿者种植一捆白杨树苗用时仍为 小时,而每名志愿者种植一捆沙棘树苗实际用时
小时,而每名志愿者种植一捆沙棘树苗实际用时 小时,于是从A组抽调6名志愿者加入B组继续种植,求植树活动所持续的时间.
小时,于是从A组抽调6名志愿者加入B组继续种植,求植树活动所持续的时间.
已知命题p: ,
,
命题q: .
.
若“p且q”为真命题,求实数m的取值范围.
已知函数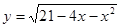 的定义域为A,函数
的定义域为A,函数 的定义域为B,(1) 若
的定义域为B,(1) 若 ,求实数
,求实数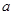 的取值范围;(2)若
的取值范围;(2)若 ,求实数
,求实数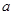 的取值范围.
的取值范围.