(本小题满分13分)已知函数 ,
,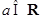 .
.
(Ⅰ)若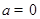 ,对于任意的
,对于任意的 ,求证:
,求证: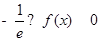 ;
;
(Ⅱ)若函数 在其定义域内不是单调函数,求实数
在其定义域内不是单调函数,求实数 的取值范围.
的取值范围.
对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如下.
(1)求 ,并根据图中的数据,用分层抽样的方法抽取
,并根据图中的数据,用分层抽样的方法抽取 个元件,元件寿命落在
个元件,元件寿命落在 之间的应抽取几个?
之间的应抽取几个?
(2)从(1)中抽出的寿命落在 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个元件寿命落在
个元件,求事件“恰好有一个元件寿命落在 之间,一个元件寿命落在
之间,一个元件寿命落在 之间”的概率.
之间”的概率.
从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:
| 分组(重量) |
 |
 |
 |
 |
| 频数(个) |
5 |
10 |
20 |
15 |
(1)根据频数分布表计算苹果的重量在 的频率;
的频率;
(2)用分层抽样的方法从重量在 和
和 的苹果中共抽取4个,其中重量在
的苹果中共抽取4个,其中重量在 的有几个?
的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在 和
和 中各有1个的概率.
中各有1个的概率.
城市公交车的数量若太多则容易造成资源的浪费;若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:分钟):
| 组别 |
候车时间 |
人数 |
| 一 |
 |
2 |
| 二 |
 |
6 |
| 三 |
 |
4 |
| 四 |
 |
2 |
| 五 |
 |
1 |
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中任选2人作进一步的调查,求抽到的两人恰好来自不同组的概率.
某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)指出这组数据的众数和中位数;
(2)若幸福指数不低于9.5分,则称该人的幸福指数为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 的分布列及数学期望.
的分布列及数学期望.
一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n。如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验。
假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为,且各件产品是否为优质品相互独立
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望。