问题提出：平面内不在同一条直线上的三点确定一个圆．那么平面内的四点（任意三点均不在同一直线上），能否在同一个圆呢？
初步思考：设不在同一条直线上的三点A、B、C确定的圆为⊙O．
（1）当C、D在线段AB的同侧时，
如图①，若点D在⊙O上，此时有∠ACB＝∠ADB，理由是 ；
如图②，若点D在⊙O内，此时有∠ACB ∠ADB；
如图③，若点D在⊙O外，此时有∠ACB ∠ADB．（填“＝”、“＞”或“＜”）；
由上面的探究，请直接写出A、B、C、D四点在同一个圆上的条件： ．
类比学习：（2）仿照上面的探究思路，请探究：当C、D在线段AB的异侧时的情形．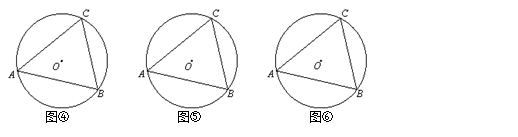
如图④，此时有 ，
如图⑤，此时有 ，
如图⑥，此时有 ．
由上面的探究，请用文字语言直接写出A、B、C、D四点在同一个圆上的条件：
．
拓展延伸：（3）如何过圆上一点，仅用没有刻度的直尺，作出已知直径的垂线？
已知：如图，AB是⊙O的直径，点C在⊙O上．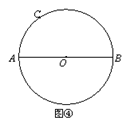
求作：CN⊥AB．
作法：①连接CA，CB；
②在
上任取异于B、C的一点D，连接DA，DB；
③DA与CB相交于E点，延长AC、BD，交于F点；
④连接F、E并延长，交直径AB于M；
⑤连接D、M并延长，交⊙O于N．连接CN．则CN⊥AB．
请按上述作法在图④中作图，并说明CN⊥AB的理由．（提示：可以利用（2）中的结论）
在平面直角坐标系中，△ABC的边AB在x轴上，且OA＞OB，以AB为直径的圆与y轴正半轴交于点C，A、B两点的横坐标xA、xB是关于x的方程x2＋3x－4=0的两个根．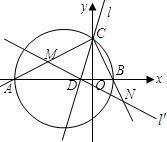
（1）求点C的坐标；
（2）若∠ACB的平分线所在的直线l交x轴于点D，求直线l对应的一次函数关系式；
（3）过点D任作一直线l′分别交射线CA、CB（点C除外）于点M、N，则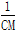
＋
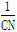的值是否为定值？若是，求出定值；若不是，请说明理由．
我们新定义一种三角形：两边平方和等于第三边平方的两倍的三角形叫做奇异三角形．
（1）根据“奇异三角形”的定义，请你判断命题“等边三角形一定是奇异三角形”是真命题还是假命题?
（2）在Rt△ABC中，∠ACB=90°，AB=c，AC=b，BC=a，且b＞a，若Rt△ABC是奇异三角形，求a：b：c；
（3）如图，AB是⊙O的直径，点C是⊙O上一点（不与点A，B重合），D是半圆 
的中点，C，D在直径AB的两侧，若在⊙O内存在点E，使AE=AD，CB=CE．
求证：△ACE是奇异三角形．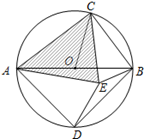
在“文化南长•全民阅读”活动中，某中学社团“清风读书社”对全校学生的人数及纸质图书阅读量（单位：本）进行了调查．2014年全校有1000名学生，2015年全校学生人数比2014年增加10%，2016年全校学生人数比2015年增加100人．
（1）2016年全校学生有 人；
（2）2015年全校学生人均阅读量比2014年多1本，阅读总量比2014年增加1700本．
（注：阅读总量=人均阅读量×人数）
①求2014年全校学生人均阅读量；
②2014年读书社人均阅读量是全校学生人均阅读量的2．5倍，如果2015年、2016年这两年读书社人均阅读量都比前一年增长一个相同的百分数a，2016年全校学生人均阅读量比2014年增加的百分数也是a，那么2016年读书社全部80名成员的阅读总量将达到全校学生阅读总量的25%，求a的值．
如图，AC是⊙O的直径，PB切⊙O于点D，交AC的延长线于点B，且∠DAB＝∠B．
（1）求∠B的度数；
（2）若BD＝9，求BC的长．
如图，在矩形ABCD中， CF⊥BD分别交BD、AD于点E、F．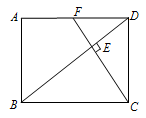
（1）求证：△DEC ∽ △FDC；
（2）若DE＝2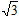
，F为AD的中点，求BD的长度．