(本小题满分14分)已知函数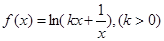 在
在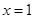 处取得极小值.
处取得极小值.
(1)求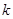 的值;
的值;
(2)若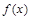 在
在 处的切线方程为
处的切线方程为 ,求证:当
,求证:当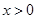 时,曲线
时,曲线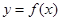 不可能在直线
不可能在直线 的下方;
的下方;
(3)若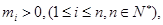 且
且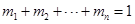 ,
,
试比较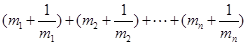 与
与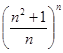 的大小,并证明你的结论.
的大小,并证明你的结论.
如图,四棱锥 中,底面
中,底面 是平行四边形,
是平行四边形, 平面
平面 ,垂足为
,垂足为 ,
, 在线段
在线段 上,
上, ,
, ,
, ,
,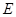 是
是 的中点,四面体
的中点,四面体 的体积为
的体积为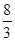 .
.
(1)求异面直线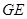 与
与 所成角的余弦值;
所成角的余弦值;
(2)棱 上是否存在点
上是否存在点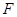 ,使
,使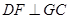 ,若存在,求
,若存在,求 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
如图, 的顶点
的顶点 ,
,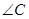 的平分线
的平分线 所在直线方程为
所在直线方程为 ,
,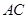 边上的高
边上的高 所在直线方程为
所在直线方程为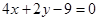 .
.
(1)求顶点 的坐标;
的坐标;
(2)求 的面积.
的面积.
设函数 .
.
(1)若曲线 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值;
(2)求函数 的单增区间;
的单增区间;
(3)若函数 有两个极值点
有两个极值点 ,求证:
,求证: .
.
已知数列 的前
的前 项和
项和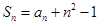 ,数列
,数列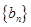 满足
满足 .
.
(1)求 ;
;
(2)设 为数列
为数列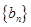 的前
的前 项和,求
项和,求 ,并求满足
,并求满足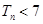 时
时 的最大值.
的最大值.
如图,菱形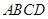 的边长为6,
的边长为6,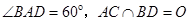 .将菱形
.将菱形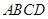 沿对角线
沿对角线 折起,得到三棱锥
折起,得到三棱锥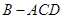 ,点
,点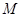 是棱
是棱 的中点,
的中点, .
.
(1)求证: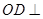 面
面 ;
;
(2)求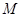 到平面
到平面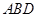 的距离.
的距离.