(本小题满分12分)已知等比数列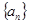 的首项
的首项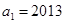 ,公比
,公比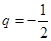 ,数列
,数列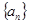 前
前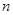 项的积记为
项的积记为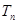 .
.
(1)求使得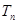 取得最大值时
取得最大值时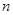 的值;
的值;
(2)证明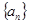 中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差按从小到大的顺序依次设为
中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差按从小到大的顺序依次设为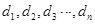 ,证明:数列
,证明:数列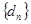 为等比数列.(参考数据
为等比数列.(参考数据 )
)
(本小题满分12分)
在数列 中,已知
中,已知
(Ⅰ)求证:数 列
列 是等比数列;
是等比数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)求数列 的前
的前 项和
项和
解:
(本小题满分12分)
用黄、蓝、白三种颜色粉刷 间办公室
间办公室
(Ⅰ) 若每间办公室刷什么颜色不要求,有多少种不同的粉刷方法?
(Ⅱ)若一种颜色粉刷 间,一种颜色粉刷
间,一种颜色粉刷 间,一种颜色粉刷
间,一种颜色粉刷 间,有多少种不同的粉刷方法?
间,有多少种不同的粉刷方法?
(Ⅲ)若每种颜色至少用一次,粉刷这 间办公室,有多少种不同的粉刷方法?
间办公室,有多少种不同的粉刷方法?
(本小题满分12分)
学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有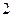 人,会跳舞的
人,会跳舞的
有 人,现从中任选
人,现从中任选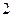 人.设
人.设 为选出的人中既会唱
为选出的人中既会唱 歌又会跳舞的人数,
歌又会跳舞的人数, .
.
(Ⅰ)求文娱队的人数;
(Ⅱ)写出 的概率分布列并计算
的概率分布列并计算 .
.
(本小题满分12分)
已知 各项展开式的二项式系数之和为
各项展开式的二项式系数之和为 .
.
(Ⅰ)求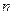 ;
;
(Ⅱ)求展开式的常数项.
(本小题满分10分)
求下列各式的极限值:
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.