已知：如图，矩形ABCD中，CD＝2，AD＝3，以C点为圆心-优题课

已知：如图，矩形ABCD中，CD＝2，AD＝3，以C点为圆心，作一个动圆，与线段AD交于点P（P和A、D不重合），过P作⊙C的切线交线段AB于F点．

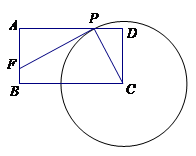
（1）求证：△CDP∽△PAF；
（2）设DP＝x，AF＝y，求y关于x的函数关系式，及自变量x的取值范围；
（3）是否存在这样的点P，使△APF沿PF翻折后，点A落在BC上，请说明理由．

科目数学题型解答题难度中等

知识点：圆幂定理相似多边形的性质

如图，四边形 $ABCD$ 中，连接 $AC$ ， $AC = AD$ ，以 $AC$ 为直径的 $⊙ O$ 过点 $B$ ，交 $CD$ 于点 $E$ ，过点 $E$ 作 $EF ⊥ AD$ 于点 $F$ ．

（1）求证： $EF$ 是 $⊙ O$ 的切线；

（2）若 $∠ BAC = ∠ DAC = 30 °$ ， $BC = 2$ ，求 $\hat{BCE}$ 的长．（结果保留 $π)$

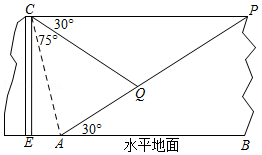
如图，某地质公园中有两座相邻小山．游客需从左侧小山山脚 $E$ 处乘坐竖直观光电梯上行100米到达山顶 $C$ 处，然后既可以沿水平观光桥步行到景点 $P$ 处，也可以通过滑行索道到达景点 $Q$ 处，在山顶 $C$ 处观测坡底 $A$ 的俯角为 $75 °$ ，观测 $Q$ 处的俯角为 $30 °$ ，已知右侧小山的坡角为 $30 °$ （图中的点 $C$ ， $E$ ， $A$ ， $B$ ， $P$ ， $Q$ 均在同一平面内，点 $A$ ， $Q$ ， $P$ 在同一直线上）

（1）求 $∠ CAP$ 的度数及 $CP$ 的长度；

（2）求 $P$ ， $Q$ 两点之间的距离．（结果保留根号）

俄罗斯足球世界杯点燃了同学们对足球运动的热情，某学校计划购买甲、乙两种品牌的足球供学生使用．已知用1000元购买甲种足球的数量和用1600元购买乙种足球的数量相同，甲种足球的单价比乙种足球的单价少30元．

（1）求甲、乙两种品牌的足球的单价各是多少元？

（2）学校准备一次性购买甲、乙两种品牌的足球共25个，但总费用不超过1610元，那么这所学校最多购买多少个乙种品牌的足球？

自我省深化课程改革以来，铁岭市某校开设了： $A$ ．利用影长求物体高度， $B$ ．制作视力表， $C$ ．设计遮阳棚， $D$ ．制作中心对称图形，四类数学实践活动课．规定每名学生必选且只能选修一类实践活动课，学校对学生选修实践活动课的情况进行抽样调查，将调查结果绘制成如下两幅不完整的统计图．

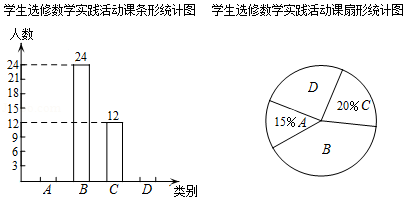
根据图中信息解决下列问题：

（1）本次共调查　　名学生，扇形统计图中 $B$ 所对应的扇形的圆心角为　　度；

（2）补全条形统计图；

（3）选修 $D$ 类数学实践活动的学生中有2名女生和2名男生表现出色，现从4人中随机抽取2人做校报设计，请用列表或画树状图法求所抽取的两人恰好是1名女生和1名男生的概率．

如图，在平面直角坐标系中，抛物线 $C_{1} : y = a x^{2} + bx - 1$ 经过点 $A (- 2, 1)$ 和点 $B (- 1, - 1)$ ，抛物线 $C_{2} : y = 2 x^{2} + x + 1$ ，动直线 $x = t$ 与抛物线 $C_{1}$ 交于点 $N$ ，与抛物线 $C_{2}$ 交于点 $M$ ．

（1）求抛物线 $C_{1}$ 的表达式；

（2）直接用含 $t$ 的代数式表示线段 $MN$ 的长；

（3）当 $ΔAMN$ 是以 $MN$ 为直角边的等腰直角三角形时，求 $t$ 的值；

（4）在（3）的条件下，设抛物线 $C_{1}$ 与 $y$ 轴交于点 $P$ ，点 $M$ 在 $y$ 轴右侧的抛物线 $C_{2}$ 上，连接 $AM$ 交 $y$ 轴于点 $K$ ，连接 $KN$ ，在平面内有一点 $Q$ ，连接 $KQ$ 和 $QN$ ，当 $KQ = 1$ 且 $∠ KNQ = ∠ BNP$ 时，请直接写出点 $Q$ 的坐标．