(本小题满分10分)选修4-1:几何证明选讲
已知在 中,
中,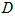 是
是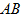 上一点,
上一点,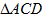 的外接圆交
的外接圆交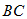 于
于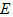 ,
,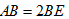 .
.
(1)求证: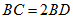 ;
;
(2)若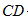 平分
平分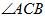 ,且
,且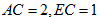 ,求
,求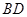 的长.
的长.
假设关于某市房屋面积 (平方米)与购房费用
(平方米)与购房费用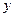 (万元),有如下的统计数据:
(万元),有如下的统计数据:
| x(平方米) |
80 |
90 |
100 |
110 |
| y(万元) |
42 |
46 |
53 |
59 |
由资料表明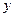 对
对 呈线性相关。
呈线性相关。
(1)求回归直线方程;
(2)若在该市购买120平方米的房屋,估计购房费用是多少?
公式:
某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段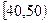 ,
, …
… 后画出如下频率分布直方图.观察图形的信息,回答下列问题:
后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)估计这次考试的众数m与中位数n(结果保留一位小数);
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和平均分.
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
已知p: 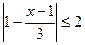 ,q:
,q:  ,若
,若 是
是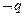 的必要不充分条件,
的必要不充分条件, 求实数
求实数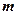 的取值范围。
的取值范围。
如图所示,两条异面直线AB,CD与三个平行平面α,β,γ分别相交于A,E,B及
C,F,D,又AD、BC与平面β的交点为H,G.
求证:四边形EHFG为平行四边形。