如图，在平面直角坐标系中，抛物线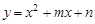
经过点A（3，0）、B（0，－3），点P是直线AB上的动点，过点P作x轴的垂线交抛物线于点M，设点P的横坐标为t．
（1）分别求出直线AB和这条抛物线的解析式．
（2）若点P在第四象限，连接AM、BM，当线段PM最长时，求△ABM的面积．
（3）是否存在这样的点P，使得以点P、M、B、O为顶点的四边形为平行四边形？若存在，请直接写出点P的横坐标；若不存在，请说明理由
数学课上，李老师出示了这样一道题目：如图
，正方形
的边长为
，
为边
延长线上的一点，
为
的中点，的垂直平分线交边
于
，交边
的延长线于
.当
时，
与
的比值是多少？
经过思考，小明展示了一种正确的解题思路：过作直线平行于交，分别于
，
，如图
，则可得：
，因为
，所以
.可求出
和
的值，进而可求得与的比值.
(1) 请按照小明的思路写出求解过程.
(2) 小东又对此题作了进一步探究，得出了
的结论.你认为小东的这个结论正确吗？如果正确，请给予证明；如果不正确，请说明理由.
某市在道路改造过程中，需要铺设一条长为1000米的管道，决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米，且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.
（1）甲、乙工程队每天各能铺设多少米？
（2）如果要求完成该项工程的工期不超过10天，那么为两工程队分配工程量（以百米为单位）的方案有几种？请你帮助设计出来.
如图，正比例函数
的图象与反比例函数
在第一象限的图象交于
点，过点作
轴的垂线，垂足为
，已知
的面积为1.
（1）求反比例函数的解析式；
（2）如果
为反比例函数在第一象限图象上的点（点与点
不重合），且点的横坐标为1，在轴上求一点
，使
最小.
如图，
为
外接圆的直径，
，垂足为点
，
的平分线交于点
，连接
，
.
(1) 求证：
；
(2) 请判断
，，
三点是否在以
为圆心，以
为半径的圆上？并说明理由.
观察下面的变形规律：
＝1－
； 
＝－
；
＝－
；……
解答下面的问题：
（1）若n为正整数，请你猜想
＝ ；
（2）证明你猜想的结论；
（3）求和：＋＋＋…＋
.