如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1)求证:AA1⊥平面ABC;
(2)求二面角A1-BC1-B1的余弦值;
(3)证明:在线段BC1存在点D,使得AD⊥A1B,并求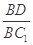 的值.
的值.
已知过原点的动直线
与圆
相交于不同的两点
.
(1)求圆
的圆心坐标;
(2)求线段
的中点
的轨迹
的方程;
(3)是否存在实数
,使得直线
与曲线
只有一个交点?若存在,求出
的取值范围;若不存在,说明理由.
设
,函数
.
(1)求
的单调区间;
(2)证明
在
上仅有一个零点;
(3)若曲线
在点
处的切线与
轴平行,且在点
处的切线与直线
平行,(
是坐标原点),证明:
.
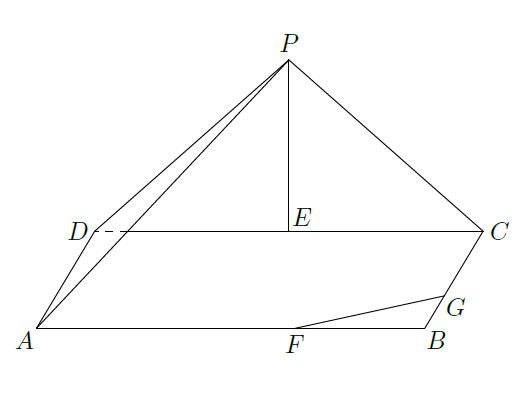
如图,三角形
所在的平面与长方形
所在的平面垂直,
,
,
,点
是
的中点,点
、
分别在线段
、
上,且
,
.
(1)证明:
;
(2)求二面角
的正切值;
(3)求直线
与直线
所成角的余弦值.
某工厂36名工人年龄数据如图: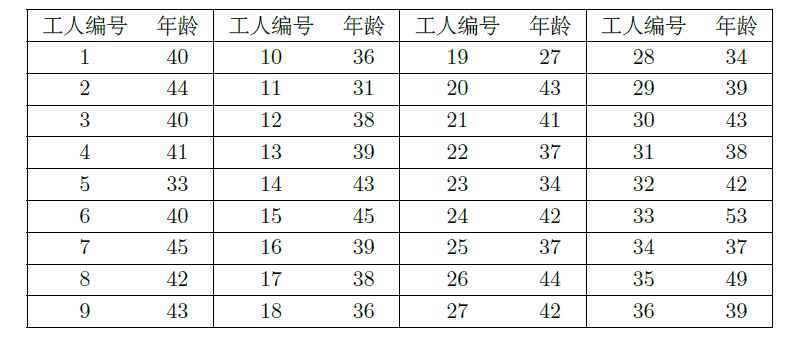
(1)用系统抽样法从36名工人中抽取容量为9的样本,且在第一分段里用随机抽样法抽到的年龄数据为44,列出样本的年龄数据;
(2)计算(1)中样本的均值
和方差
;
(3)36名工人中年龄在
﹣
和
+
之间有多少人?所占百分比是多少(精确到
)?
在平面直角坐标系 中,已知向量 .
(1)若
,求
的值;
(2)若
与
的夹角为
,求
的值.