已知椭圆G: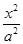 +
+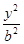 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为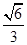 ,右焦点为(2
,右焦点为(2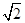 ,0).斜率为1的直线l与椭圆G交于A,B两点,以AB为底边作等腰三角形,顶点为P(-3,2).
,0).斜率为1的直线l与椭圆G交于A,B两点,以AB为底边作等腰三角形,顶点为P(-3,2).
(1)求椭圆G的方程;
(2)(有一点难度哦)求△PAB的面积.
设函数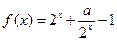 (a为实数)
(a为实数)
(1)当a=0时,若函数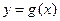 的图象与
的图象与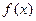 的图象关于直线x=1对称,求函数
的图象关于直线x=1对称,求函数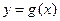 的解析式;
的解析式;
(2)当a<0时,求关于x的方程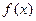 =0在实数集R上的解.
=0在实数集R上的解.
已知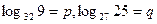 ,试用p,q表示lg5.
,试用p,q表示lg5.
增城市数、理、化竞赛时,高一某班有24名学生参加数学竞赛,28名学生参加物理竞赛,19名学生参加化学竞赛,其中参加数、理、化三科竞赛的有7名,只参加数、物两科的有5名,只参加物、化两科的有3名,只参加数、化两科的有4名。若该班学生共有48名,问没有参加任何一科竞赛的学生有多少名?
已知定义在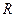 上的奇函数
上的奇函数 在
在 处取得极值.
处取得极值.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)试证:对于区间 上任意两个自变量的值
上任意两个自变量的值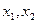 ,都有
,都有 成立;
成立;
(Ⅲ)若过点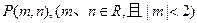 可作曲线
可作曲线 的三条切线,试求点P对应平面区域的面积.
的三条切线,试求点P对应平面区域的面积.
设 ,函数
,函数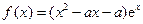 .
.
(Ⅰ)若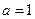 ,求曲线
,求曲线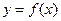 在点
在点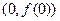 处的切线方程;
处的切线方程;
(Ⅱ)求函数 在
在 上的最小值.
上的最小值.