已知函数 (其中
(其中 是自然对数的底数),
是自然对数的底数), ,
, .
.
(1)记函数 ,且
,且 ,求
,求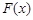 的单调增区间;
的单调增区间;
(2)若对任意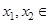
 ,
, ,均有
,均有 成立,求实数
成立,求实数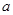 的取值范围.
的取值范围.
已知关于x的一次函数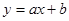 ,
,
(1)设集合P={-2,-1,1,2,3}和Q={-2,0,3},分别从集合P和Q中随机取一个数作为a和b,求函数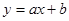 是增函数的概率;
是增函数的概率;
(2)实数a,b满足条件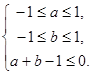 求函数
求函数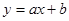 的图象经过二、三、四象限的概率.
的图象经过二、三、四象限的概率.
在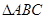 中,
中,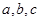 分别是角
分别是角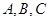 的对边,且
的对边,且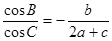 .
.
(1)求角B的大小;
(2)若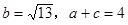 ,求
,求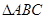 的面积.
的面积.
如图,在四棱锥P一ABCD中,平面PAD⊥平面ABCD,AB∥DC,
△PAD是等边三角形,已知AD=4,BD= ,AB=2CD=8.
,AB=2CD=8.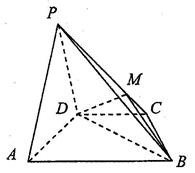
(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?请证明你的结论;
(3)求四棱锥P—ABCD的体积.
已知点(1,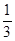 )是函数
)是函数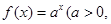 且
且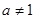 )的图象上一点,等比数列
)的图象上一点,等比数列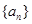 的前n项和为
的前n项和为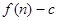 ,数列
,数列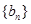
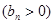 的首项为c,且前n项和
的首项为c,且前n项和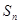 满足
满足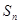 -
-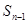 =
=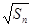 +
+ (n
(n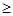 2).
2).
(1)求数列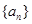 和
和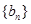 的通项公式;
的通项公式;
(2)若数列{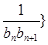 前n项和为
前n项和为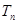 ,问
,问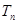 >
>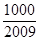 的最小正整数n是多少?
的最小正整数n是多少?
如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为2的正方形,PA=AD,F为PD的中点.
(1)求证:AF⊥平面PDC;
(2)求直线AC与平面PCD所成角的大小.