现有5道题,其中3道甲类题,2道乙类题,张同学从中任取2道题解答.试求:
(1)所取的2道题都是甲类题的概率;
(2)所取的2道题不是同一类题的概率.
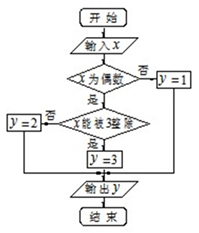
某算法的程序框图如图所示,其中输入的变量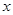 在
在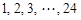 这
这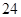 个整数中等可能随机产生.分别求出按程序框图正确编程运行时输出
个整数中等可能随机产生.分别求出按程序框图正确编程运行时输出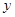 的值为
的值为 的概率
的概率 ;
;
(本小题满分16分)已知函数 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若函数 在区间
在区间 上的最小值为0,求
上的最小值为0,求 的值;
的值;
(Ⅲ)若对于任意 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分16分)椭圆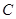 :
: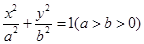 的右焦点为
的右焦点为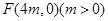 且
且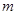 为常数,离心率为
为常数,离心率为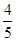 ,过焦点
,过焦点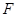 、倾斜角为
、倾斜角为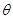 的直线
的直线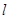 交椭圆
交椭圆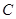 与M,N两点,
与M,N两点,
(1)求椭圆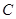 的标准方程;
的标准方程;
(2)当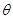 =
=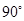 时,
时,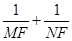 =
=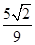 ,求实数
,求实数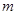 的值;
的值;
(3)试问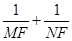 的值是否与直线
的值是否与直线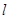 的倾斜角
的倾斜角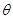 的大小无关,并证明你的结论。
的大小无关,并证明你的结论。
(本小题满分16分)已知函数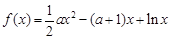 ,
, 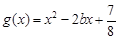 .
.
(Ⅰ)当 时,求曲线
时,求曲线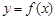 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当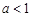 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅲ)当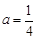 时,函数
时,函数 在
在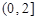 上的最大值为
上的最大值为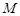 ,若存在
,若存在 ,使得
,使得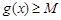 成立,求实数b的取值范围.
成立,求实数b的取值范围.