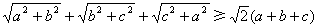（本小题满分12分）2014年APEC峰会于11月10-11日在北京召开．据志愿服务联合会的统计显示：APEC领导人会议周期间，2000名志愿者共上岗服务11219人次，累计服务132022小时，所有的志愿者来自全国四大地理区域，数据如下表所示：
| 地理区域 |
北方地区 |
南方地区 |
西北地区 |
青藏地区 |
| 志愿者人数 |
600 |
800 |
400 |
200 |
为了更进一步了解有关信息，采用分层抽样的方法从上述四大地理区域的志愿者中随机抽取50名参加问卷调查．
（Ⅰ）从参加问卷调查的50名志愿者中随机抽取两名，求这两名来自同一地理区域的概率；
（Ⅱ）在参加问卷调查的50名志愿者中，从来自北方地区、西北地区的志愿者中随机抽取两名，用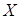
表示抽得北方地区志愿者的人数，求
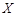的分布列和数学期望．
平面直角坐标系xOy中，过椭圆M：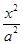
＋
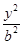＝1(a＞b＞0)右焦点的直线x＋y－
＝0交M于A，B两点，P为AB的中点，且OP的斜率为
.
(1)求M的方程；
(2)（能力提升）C，D为M上两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值．
在直角坐标系
中，点
到点
，
的距离之和是
，点的轨迹是
，直线
与轨迹交于不同的两点
和
．
（1）求轨迹的方程；
（2）是否存在常数
，
？若存在，求出的值；若不存在，请说明理由．
已知双曲线
，过点 A（2，1）的直线与已知双曲线交于P、Q两点
（1）求PQ中点的轨迹方程；
（2）过B（1，1）能否作直线
，使与所给双曲线交于两点M、N，且B为MN的中点，若存在，求出的方程，不存在说明理由
已知椭圆G：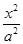
＋
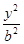＝1（a＞b＞0）的离心率为
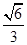，右焦点为（2
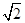，0）．斜率为1的直线l与椭圆G交于A，B两点，以AB为底边作等腰三角形，顶点为P（－3,2）．
（1）求椭圆G的方程；
（2）（有一点难度哦）求△PAB的面积．
已知a、b、c∈R，求证：