已知椭圆的中心为原点,焦点在 轴上,离心率为
轴上,离心率为 ,且经过点
,且经过点 ,直线
,直线 交椭圆于异于M的不同两点
交椭圆于异于M的不同两点 .直线
.直线 轴分别交于点
轴分别交于点 .
.
(1)求椭圆标准方程;
(2)求 的取值范围;
的取值范围;
(3)证明 是等腰三角形.
是等腰三角形.
(本小题满分12分)
某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(量大供应量)如下表所示:
 产品 产品消耗量 资源 |
甲产品(每吨) |
乙产品(每吨) |
资源限额(每天) |
| 煤(t) |
9 |
4 |
360 |
| 电力(kw·h) |
4 |
5 |
200 |
| 劳动力(个) |
3 |
10 |
300 |
| 利润(万元) |
6 |
12 |
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
(本小题满分12分)
在△ABC中,角A、B、C的对边分别为a、b、c.已知a+b=5,c=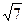 ,
,
且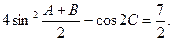
(1)求角C的大小;
(2)求△ABC的面积.
(本小题满分14分)
设函数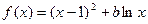 ,其中
,其中 为常数.
为常数.
(1)当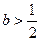 时,判断函数
时,判断函数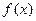 在定义域上的单调性;
在定义域上的单调性;
(2)若函数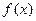 的有极值点,求
的有极值点,求 的取值范围及
的取值范围及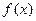 的极值点;
的极值点;
(3)求证对任意不小于3的正整数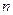 ,不等式
,不等式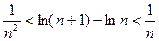 都成立.
都成立.
((本小题满分14分)
数列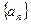 是以
是以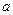 为首项,
为首项,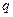 为公比的等比数列.令
为公比的等比数列.令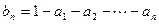 ,
,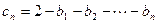 ,
,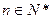 .
.
(1)试用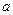 、
、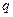 表示
表示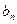 和
和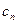 ;
;
(2)若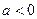 ,
,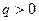 且
且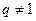 ,试比较
,试比较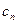 与
与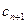 的大小;
的大小;
(3)是否存在实数对 ,其中
,其中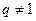 ,使
,使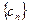 成等比数列.若存在,求出实数对
成等比数列.若存在,求出实数对 和
和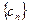 ;若不存在,请说明理由.
;若不存在,请说明理由.
(本小题满分14分)
已知抛物线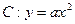 (
(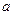 为非零常数)的焦点为
为非零常数)的焦点为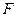 ,点
,点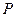 为抛物线
为抛物线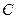 上一个动点,过点
上一个动点,过点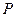 且与抛物线
且与抛物线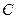 相切的直线记为
相切的直线记为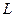 .
.
(1)求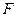 的坐标;
的坐标;
(2)当点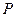 在何处时,点
在何处时,点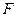 到直线
到直线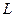 的距离最小?
的距离最小?