在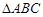 中,
中,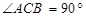 ,
,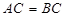 ,直线
,直线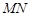 经过点
经过点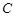 ,且
,且 于
于 ,
, 于
于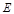 .
.
(1)当直线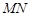 绕点
绕点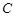 旋转到图1的位置时,求证:
旋转到图1的位置时,求证:
①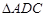 ≌
≌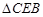 ;
;
② ;
;
(2)当直线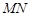 绕点
绕点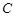 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
如图,抛物线 与直线 相交于点 和点 .
(1)求 和 的值;
(2)求点 的坐标,并结合图象写出不等式 的解集;
(3)点 是直线 上的一个动点,将点 向左平移3个单位长度得到点 ,若线段 与抛物线只有一个公共点,直接写出点 的横坐标 的取值范围.

猕猴嬉戏是王屋山景区的一大特色,猕猴玩偶非常畅销.小李在某网店选中 , 两款猕猴玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:
|
类别 价格 |
款玩偶 |
款玩偶 |
|
进货价(元 个) |
40 |
30 |
|
销售价(元 个) |
56 |
45 |
(1)第一次小李用1100元购进了 , 两款玩偶共30个,求两款玩偶各购进多少个.
(2)第二次小李进货时,网店规定 款玩偶进货数量不得超过 款玩偶进货数量的一半.小李计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?
(3)小李第二次进货时采取了(2)中设计的方案,并且两次购进的玩偶全部售出,请从利润率的角度分析,对于小李来说哪一次更合算?
(注:利润率
在古代,智慧的劳动人民已经会使用“石磨”,其原理为在磨盘的边缘连接一个固定长度的“连杆”,推动“连杆”带动磨盘转动,将粮食磨碎,物理学上称这种动力传输工具为“曲柄连杆机构”.
小明受此启发设计了一个“双连杆机构”,设计图如图1,两个固定长度的“连杆” , 的连接点 在 上,当点 在 上转动时,带动点 , 分别在射线 , 上滑动, .当 与 相切时,点 恰好落在 上,如图2.
请仅就图2的情形解答下列问题.
(1)求证: ;
(2)若 的半径为5, ,求 的长.

开凿于北魏孝文帝年间的龙门石窟是中国石刻艺术瑰宝,卢舍那佛像是石窟中最大的佛像.某数学活动小组到龙门石窟景区测量这尊佛像的高度.如图,他们选取的测量点 与佛像 的底部 在同一水平线上.已知佛像头部 为 ,在 处测得佛像头顶部 的仰角为 ,头底部 的仰角为 ,求佛像 的高度(结果精确到 .参考数据: , , .

如图,大、小两个正方形的中心均与平面直角坐标系的原点 重合,边分别与坐标轴平行,反比例函数 的图象与大正方形的一边交于点 ,且经过小正方形的顶点 .
(1)求反比例函数的解析式;
(2)求图中阴影部分的面积.
