如图所示,有一块半径长为1米的半圆形钢板,现要从中截取一个内接等腰 梯形部件ABCD,设梯形部件ABCD的面积为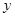 平方米.
平方米.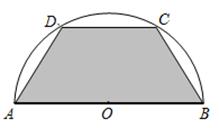
(1)按下列要求写出函数关系式:
①设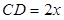 (米),将
(米),将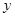 表示成
表示成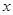 的函数关系式;
的函数关系式;
②设 ,将
,将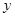 表示成
表示成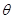 的函数关系式.
的函数关系式.
(2)求梯形部件ABCD面积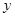 的最大值.
的最大值.
设函数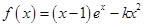 (其中
(其中 ).
).
(1) 当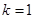 时,求函数
时,求函数 的单调区间;
的单调区间;
(2) 当 时,求函数
时,求函数 在
在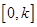 上的最大值
上的最大值 .
.
已知圆C的方程为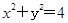 ,过点M(2,4)作圆C的两条切线,切点分别为A,B,
,过点M(2,4)作圆C的两条切线,切点分别为A,B,
直线AB恰好经过椭圆T: (a>b>0)的右顶点和上顶点.
(a>b>0)的右顶点和上顶点.
(1)求椭圆T的方程;
(2)已知直线l:y=kx+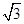 (k>0)与椭圆T相交于P,Q两点,O为坐标原点,
(k>0)与椭圆T相交于P,Q两点,O为坐标原点,
求△OPQ面积的最大值.
如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB//CD,AB=AD=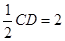 ,点M在线段EC上且不与E、C垂合.
,点M在线段EC上且不与E、C垂合.
(1)当点M是EC中点时,求证:BM//平面ADEF;
(2)当平面BDM与平面ABF所成锐二面角的余弦值为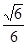 时,求三棱锥M—BDE的体积
时,求三棱锥M—BDE的体积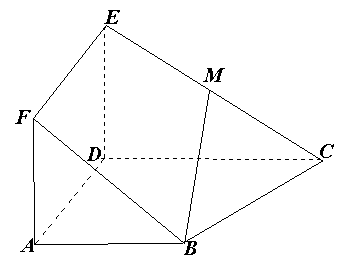
已知等比数列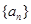 满足
满足 且
且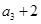 是
是 的等差中项
的等差中项
(1)求数列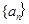 的通项公式;(2)若
的通项公式;(2)若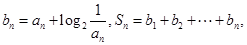 求使
求使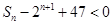 成立的正整数
成立的正整数 的最小值.
的最小值.
在某大学自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级. 某考场考生两科的考试成绩的数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人. 
(1)求该考场考生中“阅读与表达”科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分.
(i)求该考场考生“数学与逻辑”科目的平均分;
(ii)若该考场共有10人得分大于7分,其中有2人10分,2人9分, 6人8分. 从这10中随机抽取两人,求两人成绩之和大于等于18的概率.