小亮用50元钱买了10枝钢笔,准备以一定的价格出售,如果每枝钢笔以6元的价格为标准,超过的记作正数,不足的记作负数,记录如下:0.5,0.7,-1,-1.5,0.8,1,-1.5,-2,1.9,0.9
(1)这10枝钢笔的最高的售价和最低的售价各是几元?
(2)当小亮卖完钢笔后是盈还是亏?
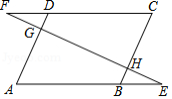
如右图,在 中, 、 分别是 、 延长线上的点,且 ,连接 交 、 于点 、 .求证: .
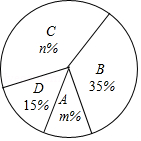
今年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为 , , , 四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
|
等级 |
成绩 |
频数(人数) |
|
|
|
4 |
|
|
|
|
|
|
|
16 |
|
|
|
6 |
根据以上信息,解答以下问题:
(1)表中的 ;
(2)扇形统计图中 , , 等级对应的扇形的圆心角为 度;
(3)该校准备从上述获得 等级的四名学生中选取两人做为学校“五好小公民”志愿者,已知这四人中有两名男生(用 , 表示)和两名女生(用 , 表示),请用列表或画树状图的方法求恰好选取的是 和 的概率.
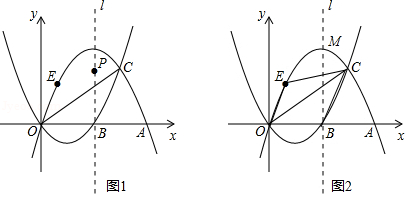
如图1,抛物线 与 相交于点 、 , 与 分别交 轴于点 、 ,且 为线段 的中点.
(1)求 的值;
(2)若 ,求 的面积;
(3)抛物线 的对称轴为 ,顶点为 ,在(2)的条件下:
①点 为抛物线 对称轴 上一动点,当 的周长最小时,求点 的坐标;
②如图2,点 在抛物线 上点 与点 之间运动,四边形 的面积是否存在最大值?若存在,求出面积的最大值和点 的坐标;若不存在,请说明理由.
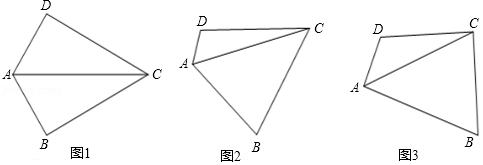
在四边形 中, ,对角线 平分 .
(1)如图1,若 ,且 ,试探究边 、 与对角线 的数量关系并说明理由.
(2)如图2,若将(1)中的条件“ ”去掉,(1)中的结论是否成立?请说明理由.
(3)如图3,若 ,探究边 、 与对角线 的数量关系并说明理由.
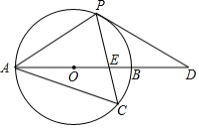
如图,以 边为直径的 经过点 , 是 上一点,连接 交 于点 ,且 , .
(1)试判断 与 的位置关系,并说明理由;
(2)若点 是弧 的中点,已知 ,求 的值.