先化简,再求值: ,其中
,其中 是不等式组
是不等式组 的整数解.
的整数解.
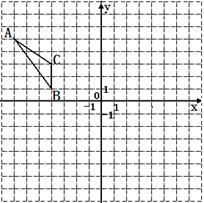
如图所示,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到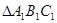 ,再将
,再将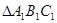 绕点
绕点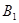 顺时针旋转90°得到
顺时针旋转90°得到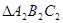 。
。
(1)作出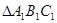 和
和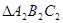 ;
;
(2)直接写出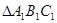 旋转时绕过的面积。
旋转时绕过的面积。
计算: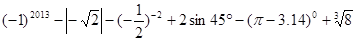
如图,在矩形ABCD中,AB=6,AD= ,点E是AD的三等分点,且AE
,点E是AD的三等分点,且AE DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为
DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为 .
.
(1)当点Q与点B重合时,求DP的长度;
(2)设AB的中点为N,PQ与线段BE相交于点M,是否存在点P,使△ 为等腰三角形?若存在,请直接写出时间
为等腰三角形?若存在,请直接写出时间 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)设△ 与四边形
与四边形 的重叠部分的面积为S,试求S与
的重叠部分的面积为S,试求S与 的函数关系式和相应的自变量
的函数关系式和相应的自变量 的取值范围.
的取值范围.
已知: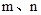 是方程
是方程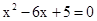 的两个实数根,且
的两个实数根,且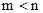 ,抛物线
,抛物线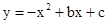 的图像经过点A(
的图像经过点A(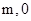 )、B(
)、B(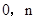 ).
).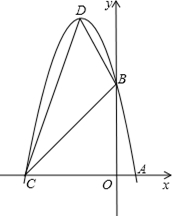
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与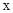 轴的另一交点为C,抛物线的顶点为D,
轴的另一交点为C,抛物线的顶点为D,
试求出点C、D的坐标和△BCD的面积;
(3)P是线段OC上的一点,过点P作PH⊥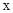 轴,与抛物线交于H点,
轴,与抛物线交于H点,
若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.