已知数列 是等差数列,其前n项和为Sn,若
是等差数列,其前n项和为Sn,若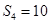 ,
,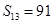 .
.
(1)求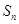 ;
;
(2)若数列{Mn}满足条件: 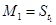 ,当
,当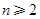 时,
时,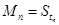 -
-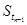 ,其中数列
,其中数列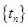 单调递增,且
单调递增,且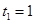 ,
,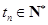 .
.
①试找出一组 ,
,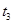 ,使得
,使得 ;
;
②证明:对于数列 ,一定存在数列
,一定存在数列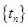 ,使得数列
,使得数列 中的各数均为一个整数的平方.
中的各数均为一个整数的平方.
已知函数
(
且
)恰有一个极大值点和一个极小值点,其中一个是
.
(Ⅰ)求函数
的另一个极值点;
(Ⅱ)求函数
的极大值
和极小值
,并求
时
的取值范围.
已知抛物线
:
,直线
交
于
两点,
是线段
的中点,过
作
轴的垂线交
于点
.
(Ⅰ)证明:抛物线
在点
处的切线与
平行;
(Ⅱ)是否存在实数
使
,求
的值;若不存在,说明理由.
三棱锥被平行于底面 的平面所截得的几何体如图所示,截面为 , , 平面 , , , , , .
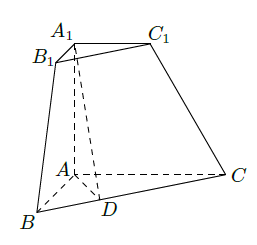
(Ⅰ)证明:平面
平面
;
(Ⅱ)求二面角
的大小.
某射击测试规则为:每人最多射击3次,击中目标即终止射击,第 次击中目标得
分,3次均未击中目标得0分.已知某射手每次击中目标的概率为0.8,其各次射击结果互不影响.
次击中目标得
分,3次均未击中目标得0分.已知某射手每次击中目标的概率为0.8,其各次射击结果互不影响.
(Ⅰ)求该射手恰好射击两次的概率;
(Ⅱ)该射手的得分记为
,求随机变量
的分布列及数学期望.
已知函数
.
(Ⅰ)求函数
的最小正周期及最值;
(Ⅱ)令
,判断函数
的奇偶性,并说明理由.