如图1,把一张长方形的纸片ABCD沿对角线BD折叠,点C落在E处,BE交AD于点F.
(1)求证:FB=FD;
(2)如图2,连接AE,求证:AE∥BD;
(3)如图3,延长BA,DE相交于点G,连接GF并延长交BD于点H,求证:GH垂直平分BD。
(1)-5×6×(- )×
)×
(2)(-24)×(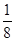 -
- +
+ )
)
(3)-12-[1 +(-12)÷6]2×(-
+(-12)÷6]2×(- )
)
我国是世界上严重缺水的国家之一,为了增强居民的节水意识,某自来水公司对居民用水采取以户为单位分段计费办法收费;即每月用水10吨以内(包括10吨)的用户,每吨水收费a元,每月用水超过10吨的部分,按每吨b元(b>a)收费,设一户居民月用水x(吨),应收水费y(元),y与x之间的函数关系如图所示.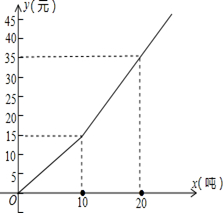
(1)分段写出y与x的函数关系式.
(2)某户居民上月用水8吨,应收水费多少元?
(3)已知居民甲上月比居民乙多用水4吨,两家一共交水费46元,求他们上月分别用水多少吨?
某景点的门票价格规定如下表
| 购票人数 |
1—50人 |
51—100人 |
100人以上 |
| 每人门票价 |
12元 |
10元 |
8元 |
某校八年(1)(2)两班共102人去游览该景点,其中(1)班不足50人,(2)班多于50人,如果两班都以班为单位分别购票,则一共付款1118元
(1)两班各有多少名学生?
(2)如果你是学校负责人,你将如何购票?你的购票方法可节省多少钱?
如图所示,已知矩形ABCD中,AD=8cm,AB=6cm,对角线AC的垂直平分线交AD于E,交BC于F.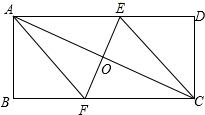
(1)试判断四边形AFCE是怎样的四边形;
(2)求出四边形AFCE的周长.
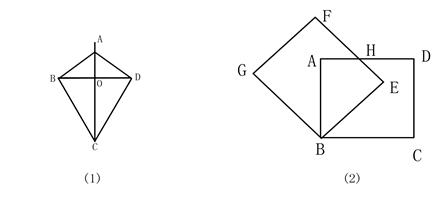
阅读下列材料:如图(1)在四边形ABCD中,若AB=AD,BC=CD,则把这样的四边形称之为“筝形”
解答问题:如图(2)将正方形ABCD绕着点B逆时针旋转一定角度后,得到正方形GBEF,边AD与EF相交于点H.请你判断四边形ABEH是否是“筝形”,说明你的理由.