[问题提出]
学习了三角形全等的判定方法(即“SAS”,“ASA”,“AAS”,“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
[初步思考]我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E.然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
[深入探究]
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据________,可以知道Rt△ABC≌Rt△DEF.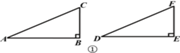
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角.求证:△ABC≌△DEF.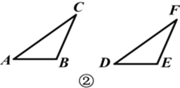
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹).
(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接填写结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,若________,则△ABC≌△DEF.
如图,⊙O的半径为6cm,将圆折叠,使点C与圆心O重合,折痕为AB,E、F是AB上两点(E、F不与A、B重合且E在F右边),且AF=BE.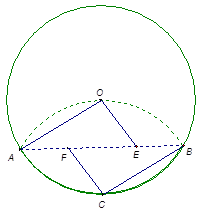
(1)判定四边形OECF的形状;
(2)AF为多少时,△CFB为直角三角形。
有一个装有进出水管的容器,单位时间内进水管与出水管的进出水量均一定,已知容器的容积为600升,图中线段OA与BC,分别表示单独打开一个进水管和单独打开一个出水管时,容器的存水量Q(升)随时间t变化的函数关系.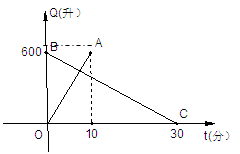
(1)求线段BC所表示的Q与t之间的函数关系式,并写出自变量t的取值范围;
(2)现已知容器内有水200升,先打开两个进水管和一个出水管一段时间,然后再关上一个进水管,直至把容器放满水,若总共用时不超过8分钟。请问,在这个过程中同时打开两个进水管和一个出水管的时间至少是多少分钟?
王老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班和(2)班进行了检测.如图表示从两班各随机抽取的10名学生的得分情况:
(1)利用图中提供的信息,补全下表:
| 班级 |
平均数(分) |
中位数(分) |
众数(分) |
| (1)班 |
24 |
24 |
|
| (2)班 |
24 |
(2)若把24分以上(含24分)记为”优秀”,两班各40名学生,请估计两班各有多少名学生成绩优秀;
(3)观察图中数据分布情况,根据方差比较哪个班的学生纠错的得分情况比较整齐.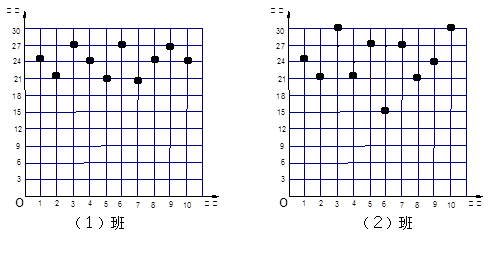
已知:如图,△ABC是等边三角形,D、E分别是BA、CA的延长线上的点,且AD=AE,连接ED并延长到F,使得EF=EC,连接AF、CF、BE.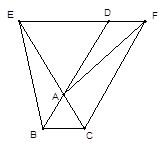
(1)求证:四边形BCFD是平行四边形;
(2)试指出图中与AF相等的线段,并说明理由。
(1)计算: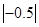 +(π-3)0-
+(π-3)0-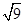 -cos60°+tan30°
-cos60°+tan30°
(2)已知x是一元二次方程
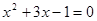 的实数根,求代数式:
的实数根,求代数式: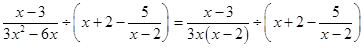 的值.
的值.