某公司欲招聘业务员一名,现对A、B、C三名候选人分别进行笔试、面试测试,成绩如下表:
| 测试项目 |
测试成绩 |
||
| 甲 |
乙 |
丙 |
|
| 笔试 |
75 |
85 |
90 |
| 面试 |
93 |
75 |
72 |
(1)如果按照三人测试成绩的平均成绩录取人选,那么谁将被录用?
(2)根据实际需要,公司想将丙录用,请兼顾笔试、面试两个方面,你确定的方案是什么?写出理由.
解方程组: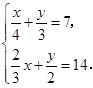
解方程组: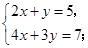
我们常用各种多边形地砖铺砌成美丽的图案,也就是说,使用给定的某些多边形,能够拼成一个平面图形,既不留一丝空白,又不互相重叠,这在几何里叫做平面密铺(镶嵌).我们知道,当围绕一点拼在一起的几个多边形的内角和为360°时,就能够拼成一个平面图形,某校研究性学习小组研究平面密铺的问题,其中在探究用两种边长相等的正多边形做平面密铺的情形时用了以下方法;
如果用x个正三角形、y个正六边形进行平面密铺,可得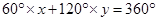 ,化简得
,化简得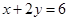 .因为x、y都是正整数,所以只有当x=2,y=2或x=4,y=1时上式才成立,即2个正三角形和2个正六边形或4个正三角形和1个正六边形可以拼成一个无缝隙、不重叠的平面图形,如图(1)、(2)、(3).
.因为x、y都是正整数,所以只有当x=2,y=2或x=4,y=1时上式才成立,即2个正三角形和2个正六边形或4个正三角形和1个正六边形可以拼成一个无缝隙、不重叠的平面图形,如图(1)、(2)、(3).
①请你依照上面的方法研究用边长相等的x个正三角形和y个正方形进行平面密铺的情形,并按图(4)中给出的正方形和正三角形的大小大致画出密铺后的图形的示意图(只要画出一种图形即可);
②如用形状、大小相同的如图(5)方格纸中的三角形,能进行平面密铺吗?若能,请在方格纸中画出密铺的设计图.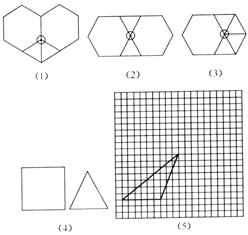
某生产厂家因工作失误,使一批正方形瓷砖的一个角都受到了同样的损坏如图所示,在有人决定将这批瓷砖全部报废时,一位技术员设计了一个合理的方案,使这批瓷砖经过简单加工后又能铺地用了,请画图表示这位技术员的设计方案.
已知,如图,在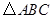 中,
中,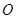 是高
是高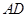 和
和 的交点,观察图形,试猜想
的交点,观察图形,试猜想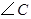 和
和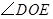 之间具有怎样的数量关系,并论证你的猜想.
之间具有怎样的数量关系,并论证你的猜想.