在平面直角坐标系xOy中,M、N分别是椭圆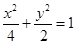 的顶点,过坐标原点的直线交椭圆于P,A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,连结AC,并延长交椭圆于点B,设直线PA的斜率为k.
的顶点,过坐标原点的直线交椭圆于P,A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,连结AC,并延长交椭圆于点B,设直线PA的斜率为k.
(1)若直线PA平分线段MN,求k的值;
(2)当k=2时,求点P到直线AB的距离d,且求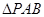 的面积
的面积 .
.
如图所示,在棱长为2的正方体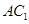 中,点
中,点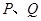 分别在棱
分别在棱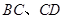 上,满足
上,满足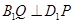 ,且
,且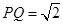 .
.
(1)试确定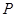 、
、 两点的位置.
两点的位置.
(2)求二面角 大小的余弦值.
大小的余弦值.
已知曲线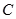 的极坐标方程为
的极坐标方程为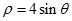 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴的非负半轴建立平面直角坐标系,并与极坐标系取相同的单位长度,直线l的参数方程为
轴的非负半轴建立平面直角坐标系,并与极坐标系取相同的单位长度,直线l的参数方程为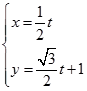 (
(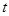 为参数),求直线l被曲线
为参数),求直线l被曲线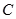 截得的线段长度.
截得的线段长度.
已知矩阵M = ,N =
,N =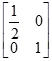 ,试求曲线
,试求曲线 在矩阵MN变换下的函数解析式.
在矩阵MN变换下的函数解析式.
在数列 中,
中,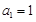 ,且对任意的
,且对任意的 ,
,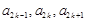 成等比数列,其公比为
成等比数列,其公比为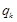 .
.
(1)若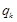 =2(
=2( ),求
),求 ;
;
(2)若对任意的 ,
,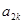 ,
,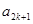 ,
,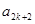 成等差数列,其公差为
成等差数列,其公差为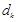 ,设
,设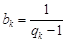 .
.
①求证: 成等差数列,并指出其公差;
成等差数列,并指出其公差;
②若 =2,试求数列
=2,试求数列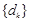 的前
的前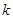 项的和
项的和 .
.
已知函数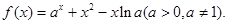
(1)求函数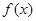 在点
在点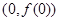 处的切线方程;
处的切线方程;
(2)求函数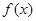 单调递增区间;
单调递增区间;
(3)若存在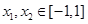 ,使得
,使得 是自然对数的底数),求实数
是自然对数的底数),求实数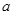 的取值范围.
的取值范围.