某校有在校高中生共1600人,其中高一学生520人,高二学生500人,高三学生580.如果想通过抽查其中的80人,来调查学生的消费情况,考虑到学生的年级高低消费情况有明显差别,而同一年级内消费情况差异较小,问应当采用怎样的抽样方法?高三学生中应抽查多少人?
某单位共有在岗职工人数为624人,为了调查工人上班时,从离开家到来到单位的路上平均所用时间,决定抽取10%的工人调查这一情况,如何采用系统抽样方法完成这一抽样?
某校有学生1200人,为了调查某种情况打算抽取一个样本容量为50的样本,问此样本若采用简单随机抽样将如何获得?
有甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40km的B处,乙厂到河岸的垂足D与A相距50km,两厂要在此岸边合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,问供水站C建在岸边何处才能使水管费用最省?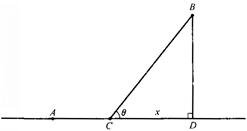
已知函数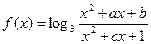 ,是否存在实数a、b、c,使
,是否存在实数a、b、c,使 同时满足下列三个条件:(1)定义域为R的奇函数;(2)在
同时满足下列三个条件:(1)定义域为R的奇函数;(2)在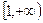 上是增函数;(3)最大值是1.若存在,求出a、b、c;若不存在,说明理由.
上是增函数;(3)最大值是1.若存在,求出a、b、c;若不存在,说明理由.