（本小题满分12分）已知函数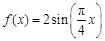
在同一半周期内的图象过点
，其中
为坐标原点，
为函数
图象的最高点，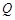
为函数的图象与
轴的正半轴的交点.
（Ⅰ）求证：
为等腰直角三角形.
（Ⅱ）将绕原点按逆时针方向旋转角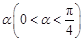
，得到
，若点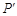
恰好落在曲线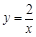
上（如图所示），试判断点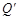
是否也落在曲线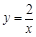上，并说明理由．
（本小题满分14分）
三棱
柱
中，
侧棱与底面垂直，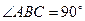
，
，
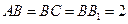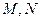分别是
，
的中点．
（1）求证：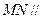
平面
；
（2）求证：
平面
；
（3）求二面角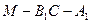
的余弦值．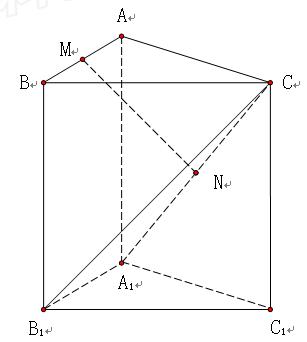
(本小题满分13分)
已知二次函数
，且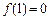
．
（1）若函数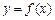
与x轴的两个交点
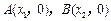之间的距离为2，求b的值；
（2）若关于x的方程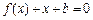
的两个实数根分别在区间
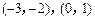内，求b的取值范围．
(本
小题满分13分)
（1）解关于x的不等式
；
（2）记(1)中不等式的解集为A，函
数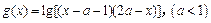
的定义域为B．若
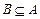，求实数a的取值范围．
函数的性质通常指函数的定义域、值域、奇偶性、单调性、周期性等，请选择适当的探究顺序，研究函数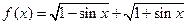
的性质，并在此基础上，作出其在
的图象
已知定义在
上的函数
的周期为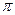
，且对一切
，都有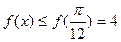
（1）求函数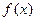
的表达式
（2）在△
中，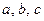
分别是角A，B，C的对边，已知
，
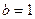，△的面积为
，求
的值