已知命题:“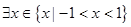 ,使等式
,使等式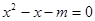 成立”是真命题.
成立”是真命题.
(1)求实数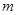 的取值集合
的取值集合 ;
;
(2)设不等式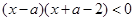 的解集为
的解集为 ,若
,若 是
是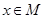 的必要条件,求
的必要条件,求 的取值范围.
的取值范围.
..(本题14分)三棱柱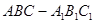 中,侧棱与底面垂直,
中,侧棱与底面垂直,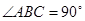 ,
,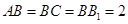 ,
,  分别是
分别是 ,
, 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求三棱锥
 的体积.
的体积.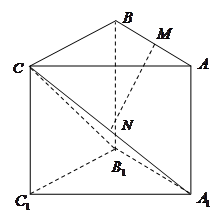
.(本题12分)为了调查某厂2000名工人生产某种产品的能力,随机抽查了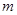 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为 ,
,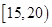 ,
,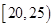 ,
,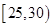 ,
,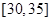 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在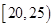 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求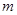 ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工人不在同一组的概率是多少?
(本题12分)在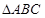 中,
中,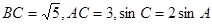
(Ⅰ)求AB的值;
(Ⅱ)求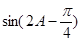 的值.
的值.
(本小题满分14分)已知数列 的前
的前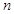 项和为
项和为 ,点
,点 在直线
在直线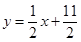 上;数列
上;数列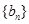 满足
满足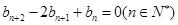 ,且
,且 ,它的前9项和为153.
,它的前9项和为153.
(1)求数列 、
、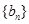 的通项公式;
的通项公式;
(2)设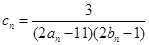 ,数列
,数列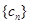 的前
的前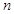 项和为
项和为 ,求使不等式
,求使不等式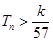 对一切
对一切 都成立的最大正整数
都成立的最大正整数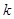 的值;
的值;
(3)设 ,是否存在
,是否存在 ,使得
,使得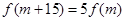 成立?若存在,求出
成立?若存在,求出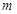 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分14分)
设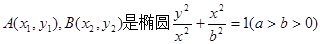 上的两点,
上的两点,
满足 ,椭圆的离心率
,椭圆的离心率 短轴长为2,0为坐标原点.
短轴长为2,0为坐标原点.
(1)求椭圆的方程;
(2)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.