(本题共12分)设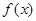 为定义在
为定义在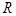 上的偶函数,当
上的偶函数,当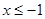 时,
时,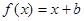 ,且
,且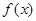 的图象经过点
的图象经过点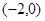 ,又在
,又在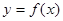 的图象中,有一部分是顶点为(0,2),且过
的图象中,有一部分是顶点为(0,2),且过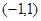 的一段抛物线。
的一段抛物线。
(1)试求出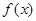 的表达式;
的表达式;
(2)求出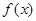 值域;
值域;
已知函数 。
。
(1)判断函数 的单调性;
的单调性;
(2)证明:
抛物线 在点P处的切线
在点P处的切线 分别交x轴、y轴于不同的两点A、B,
分别交x轴、y轴于不同的两点A、B, 。当点P在C上移动时,点M的轨迹为D。
。当点P在C上移动时,点M的轨迹为D。
(1)求曲线D的方程:
(2)圆心E在y轴上的圆与直线 相切于点P,当|PE|=|PA|,求圆的方程。
相切于点P,当|PE|=|PA|,求圆的方程。
如图,在四棱锥P—ABCD中,PA⊥底面ABCD,ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2。
(2)若∠PDC=120°,求四棱锥P—ABCD的体积。
金融机构对本市内随机抽取的20家微小企业的产业结构调整及生产经营情况进行评估,根据得分将企业评定为优秀、良好、合格、不合格四个等级,金融机构将根据等级对企业提供相应额度的资金支持。
(1)在答题卡上作出频率分布直方图,并由此估计该市微小企业所获资金支持的均值;
(2)金融机构鼓励得分前2名的两家企业A、B随机收购得分后2名的两家企业a、b中的一家,求A、B企业选择收购同一家企业的概率。
如图,为了测量河对岸A、B两点之间的距离,观察者找到一个点C,从C点可以观察到点A、B;找到一个点D,从D点可以观察到点A、C:找到一个点E,从E点可以观察到点B、C。并测得以下数据:CD=CE=100m,∠ACD=90°,∠ACB=45°,∠BCE=75°,∠CDA=∠CEB=60°,求A、B两 点之间的距离。