(本小题满分13分)在等比数列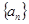 中,
中, 且
且 ,
, 是
是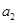 和
和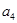 的等差中项.
的等差中项.
(Ⅰ)求数列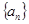 的通项公式;
的通项公式;
(Ⅱ)若数列 满足
满足 ,(
,(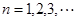 ),求数列
),求数列 的前
的前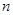 项和
项和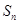 .
.
在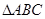 中,角
中,角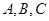 所对的边分别为
所对的边分别为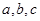 ,且
,且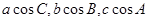 成等差数列.
成等差数列.
(1)求角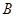 的大小;
的大小;
(2)若 ,求
,求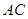 边上中线长的最小值.
边上中线长的最小值.
已知曲线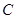 :
: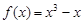
(1)试求曲线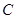 在点
在点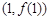 处的切线方程;
处的切线方程;
(2)试求与直线 平行的曲线C的切线方程.
平行的曲线C的切线方程.
已知:函数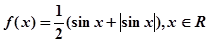
(1)求函数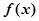 的周期T,与单调增区间.
的周期T,与单调增区间.
(2)函数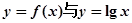 的图象有几个公共交点.
的图象有几个公共交点.
(3)设关于 的函数
的函数 的最小值为
的最小值为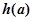 ,试确定满足
,试确定满足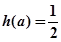 的
的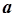 的值,并对此时的
的值,并对此时的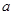 值求
值求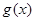 的最小值.
的最小值.
对实验中学高三年级学生参加社区服务次数进行统计,随机抽取M名学生作样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图:
(1)求出表中M,p及图中a的值;
(2)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求两人来自同一小组的概率.
如图:已知,在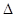 OAB中,点A是BC的中点,点D是将向量
OAB中,点A是BC的中点,点D是将向量 分为2:1的一个分点,DC和OA交于点E.设
分为2:1的一个分点,DC和OA交于点E.设 ,
,
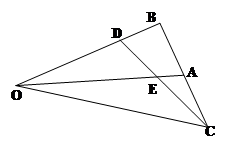
(1)用向量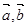 表示
表示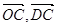 ;
;
(2)若 ,求实数
,求实数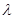 的值.
的值.