(本小题满分14分)已知离心率为 的椭圆
的椭圆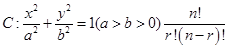 与直线
与直线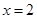 相交于
相交于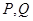 两点(点
两点(点 在
在 轴上方),且
轴上方),且 .点
.点 是椭圆上位于直线
是椭圆上位于直线 两侧的两个动点,且
两侧的两个动点,且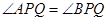 .
.
(Ⅰ)求椭圆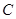 的标准方程;
的标准方程;
(Ⅱ)求四边形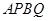 面积的取值范围.
面积的取值范围.
已知函数 ,
,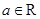 .
.
(1)当 时,求曲线
时,求曲线 在点
在点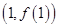 处的切线方程;
处的切线方程;
(2)当 时,求证:
时,求证: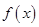 在
在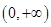 上为增函数;
上为增函数;
(3)若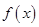 在区间
在区间 上有且只有一个极值点,求
上有且只有一个极值点,求 的取值范围.
的取值范围.
已知二次函数 (
( )的图象与
)的图象与 轴有两个不同的交点
轴有两个不同的交点 、
、 ,且
,且 .
.
(1)求 的范围;
的范围;
(2)证明 .
.
用长为
 的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为
的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为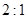 ,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
已知 .
.
(1) 是
是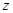 的共轭复数,求
的共轭复数,求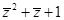 的值;
的值;
(2)类比数列的有关知识,求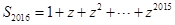 的值.
的值.
某组织对男女青年是否喜爱古典音乐进行了一个调查,调查者随机调查了 名青年,下表给出了调查结
名青年,下表给出了调查结
果(单位:人)
(1)用分层抽样的方法在不喜爱古典音乐的青年中抽 人,其中男青年应抽几人?
人,其中男青年应抽几人?
(2)男女青年喜爱古典音乐的程度是否有差异?