(本小题满分13分)已知椭圆C: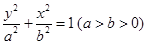 的离心率为
的离心率为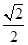 ,其四个顶点组成的菱形的面积是
,其四个顶点组成的菱形的面积是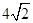 ,O为坐标原点,若点A在直线
,O为坐标原点,若点A在直线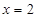 上,点B在椭圆C上,且
上,点B在椭圆C上,且 .
.
(1)求椭圆C的方程;
(2)求线段AB长度的最小值;
(3)试判断直线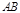 与圆
与圆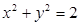 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
已知A、B、C是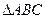 的内角,向量
的内角,向量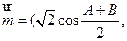

 (1)求
(1)求 ; (2)求
; (2)求
设函数f (x) =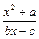 (b,c∈N*),若方程f(x) = x的解为0,2,且f (–2)<–
(b,c∈N*),若方程f(x) = x的解为0,2,且f (–2)<–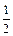 .(Ⅰ)试求函数f(x)的单调区间;(Ⅱ)已知各项不为零的数列{an}满足4Sn·f (
.(Ⅰ)试求函数f(x)的单调区间;(Ⅱ)已知各项不为零的数列{an}满足4Sn·f (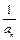 ) = 1,其中Sn为{an}的前n项和.求证:
) = 1,其中Sn为{an}的前n项和.求证: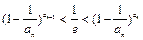 .
.
如图所示,F1、F2是双曲线x2 – y2 = 1的两个焦点,O为坐标原点,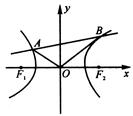
圆O是以F1F2为直径的圆,直线l:y = kx + b与圆O相切,并与双曲线交于A、B两点.
(Ⅰ)根据条件求出b和k的关系式;
(Ⅱ)当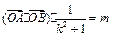 ,且满足2≤m≤4时,
,且满足2≤m≤4时,
求△AOB面积的取值范围.
已知函数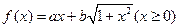 ,且函数
,且函数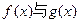 的图象关于直线
的图象关于直线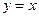 对称,又
对称,又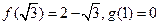 . (1)求
. (1)求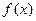 的值域;(2)是否存在实数
的值域;(2)是否存在实数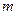 ,使命题
,使命题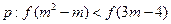 和
和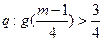 满足复合命题
满足复合命题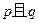 为真命题? 若存在, 求出
为真命题? 若存在, 求出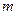 的范围; 若不存在, 说明理由.
的范围; 若不存在, 说明理由.
某商场预计2009年1月份起前x个月,顾客对某种商品的需求总量p(x)(单位:件)与x的关系近似地满足p(x)=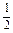 x(x+1)(39-2x),(x∈N*,且x≤12).该商品第x月的进货单价q(x)(单位:元)与x的近似关系是q(x)=150+2x.(x∈N*,且x≤12).(1)写出今年第x月的需求量f(x)件与x的函数关系式;(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问商场2009年第几月份销售该商品的月利润最大,最大月利润为多少元?
x(x+1)(39-2x),(x∈N*,且x≤12).该商品第x月的进货单价q(x)(单位:元)与x的近似关系是q(x)=150+2x.(x∈N*,且x≤12).(1)写出今年第x月的需求量f(x)件与x的函数关系式;(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问商场2009年第几月份销售该商品的月利润最大,最大月利润为多少元?