(本小题满分12分)甲乙两个学校高三年级分别有1100人,1000人,为了了解两个学校全体高三年级学生在该地区一模考试的数学成绩情况,采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩(发现两校学生的数学成绩都不低于70分),并作出了如下的频数分布统计表,规定考试成绩在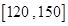 内为优秀,甲校:
内为优秀,甲校:
| 分组 |
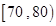 |
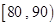 |
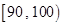 |
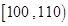 |
 |
 |
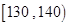 |
 |
| 频数 |
2 |
3 |
10 |
15 |
15 |
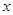 |
3 |
1 |
乙校:
| 分组 |
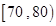 |
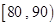 |
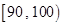 |
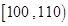 |
 |
 |
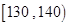 |
 |
| 频数 |
1 |
2 |
9 |
8 |
10 |
10 |
 |
3 |
(Ⅰ)计算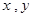 的值;
的值;
(Ⅱ)由以上统计数据填写下面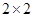 列联表,若按是否优秀来判断,是否有97.5% 的把握认为两个学校的数学成绩有差异.
列联表,若按是否优秀来判断,是否有97.5% 的把握认为两个学校的数学成绩有差异.
| |
甲校 |
乙校 |
总计 |
| 优秀 |
|
|
|
| 非优秀 |
|
|
|
| 总计 |
|
|
|
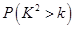 |
 |
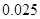 |
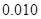 |
 |
 |
 |
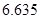 |
附:
已知函数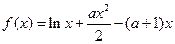 ,
,
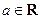 ,且
,且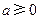 .
.
(Ⅰ)若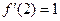 ,求
,求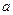 的值;
的值;
(Ⅱ)当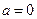 时,求函数
时,求函数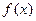 的最大值;
的最大值;
(Ⅲ)求函数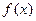 的单调递增区间.
的单调递增区间.
如图,在四棱锥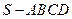 中,底面
中,底面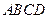 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形,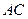 与
与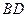 的交点为O.
的交点为O.
(Ⅰ)求证: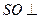 平面
平面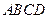 ;
;
(Ⅱ)已知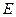 为侧棱
为侧棱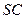 上一个动点. 试问对于
上一个动点. 试问对于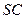 上任意一点
上任意一点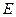 ,平面
,平面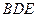 与平面
与平面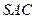 是否垂直?若垂直,请加以证明;若不垂直,请
是否垂直?若垂直,请加以证明;若不垂直,请 说明理由.
说明理由.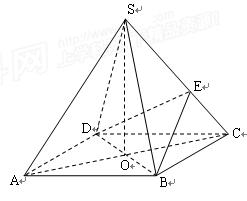
(本题满分1 3分)
3分)
某运动员进行20次射击练习,记录了他射击的有关数据,得到下表:
| 环数 |
7 |
8 |
9 |
10 |
| 命中次数 |
2 |
7 |
8 |
3 |
(Ⅰ)求此运动员射击的环数的平均数;
(Ⅱ)若将表中某一环数所对应的命中次数作为一个结果,在四个结果(2次、7次、8次、3次)中,随机取2个不同的结果作为基本事件进行研究,记这两个结果分别为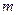 次、
次、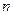 次,每个基本事件为(m,n).
次,每个基本事件为(m,n).
求“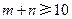 ”的概率.
”的概率.
设函数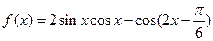 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)当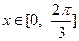 时,求函数
时,求函数 的最大值及取得最大值时的
的最大值及取得最大值时的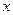 的值.
的值.
已知 是递增数列,其前
是递增数列,其前 项和为
项和为 ,
,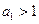 ,
, 且
且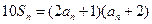 ,
,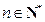 .
.
(Ⅰ)求数列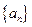 的通项
的通项 ;
;
(Ⅱ)是否存在 ,使得
,使得 成立?若存在,写出一组符合条件的
成立?若存在,写出一组符合条件的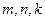 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)设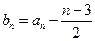 ,若对于任意的
,若对于任意的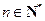 ,不等式
,不等式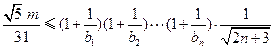 恒成立,求正整数
恒成立,求正整数 的最大值.
的最大值.