某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入。下表是某周的生产情况(超产记为正、减产记为负):
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 增减产值 |
+5 |
-2 |
-4 |
+13 |
-10 |
+16 |
-9 |
(1)根据记录的数据可知该厂星期五生产自行车_____________辆;
(2)根据记录的数据可知该厂本周实际生产自行车_____________辆;
(3)该厂实行每日计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣20元,那么该厂工人这一周的工资总额是多少元?
(4)若将上面第(3)问中“实行每日计件工资制”改为“实行每周计件工资制”, 其他条件不变,在此方式下这一周工人的工资与按日计件的工资哪一个更多?请说明理由。 ( 8分)
|
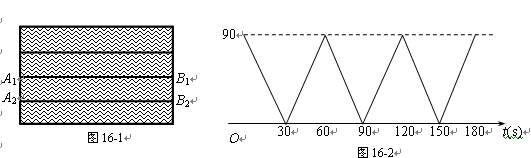
如图16-1,在一次航海模型船训练中,A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲船在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙船在赛道A2B2上以2m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两船同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲船运动时,y(m)与t(s)的函数图象如图16-2所示.
如图15,在Rt△ABC中,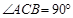 ,CP平分∠ACB,CP与AB交于点D,且 PA=PB.
,CP平分∠ACB,CP与AB交于点D,且 PA=PB.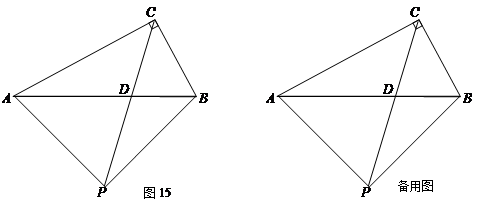
请你过点P分别向AC、BC作垂线,垂足分别为点E、F,并判断四边形PECF的形状
求证:△PAB为等腰直角三角形
设
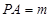 ,
,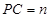 ,试用
,试用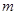 、
、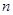 的代数式表示
的代数式表示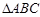 的周长;
的周长;试探索当边AC、BC的长度变化时,
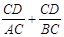 的值是否发生变化,若不变,请直接写出这个不变的值,若变化,试说明理由
的值是否发生变化,若不变,请直接写出这个不变的值,若变化,试说明理由
某校为外国留学生举办“唱汉语歌曲”比赛,设优秀奖、鼓励奖共12名,其中优秀奖不少于6名.学校购买“脸谱”和“中国结”作为奖品,优秀奖和鼓励奖分别奖励“脸谱”和“中国结”各一个,费用信息如图14所示.请求出一个“脸谱”和一个“中国结”各多少元?
若购买奖品费用不超过500元,则本次活动优秀奖和鼓励奖名额应如何设置?
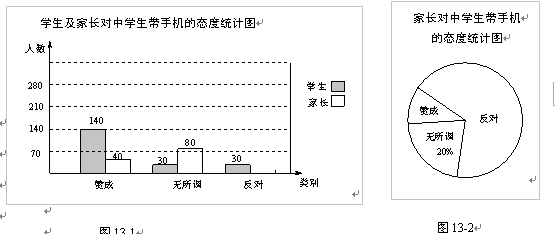
校园手机”现象越来越受到社会的关注,小记者刘凯随机调查了某校若干学生和家长对中学生带手机现象的看法,制作了如下的统计图:求这次调查的总人数,并补全图13-1
求图13-2中表示家长“赞成”的圆心角的度数;
针对随机调查的情况,刘凯决定从初三一班表示赞成的4位家长中随机选择2位进行深入调查,其中包含小亮和小丁的家长,请你利用树状图或列表的方法,求出小亮和小丁的家长被同时选中的概率.
如图12所示的8×8网格中,每个小正方形边长均为1,以这些小正方形的顶点为顶点的三角形称为格点三角形在图12中以线段AB为一边,点P为顶点且面积为6的格点三角形共有个;

请你选择(1)中的一个点P为位似中心,在图12中画出格点△A′B′P,使
△ABP与△A′B′P的位似比为2:1求tan∠PB′A′的值.