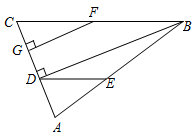
(本题12分)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= ,其中
,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
如图,是小亮晚上在广场散步的示意图,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.
(1)在小亮由B处沿BO所在的方向行走到达O处的过程中,他在地面上的影子长度的变化情况为;
(2)请你在图中画出小亮站在AB处的影子;
(3)当小亮离开灯杆的距离OB=4.2m时,身高(AB)为1.6m的小亮的影长为1.6m,问当小亮离开灯杆的距离OD=6m时,小亮的影长是多少m?
如图:已知△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P点在AC上(与A、C不重合),Q在BC上.
(1)当△PQC的面积是四边形PABQ的面积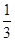 时,求CP的长.
时,求CP的长.
(2)当△PQC的周长与四边形PABQ的周长相等时,求CP的长.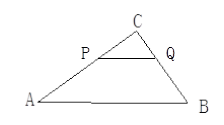
一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同.
(1)从箱子中任意摸出一个球是白球的概率是多少?
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,用列表或画树状的方法求两次摸出的球都是白球的概率.
如图,正方形AEFG的顶点E在正方形ABCD的边CD上;AD的延长线交EF于H点.
(1)试说明:△AED∽△EHD
(2)若E为CD的中点,求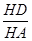 的值.
的值.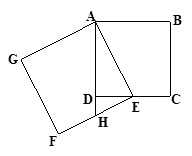
如图,BD⊥AC于D点,FG⊥AC于G点,∠CBE+∠BED=180°.
(1)求证:FG∥BD;
(2)求证:∠CFG=∠BDE.