已知:如图,在□ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
(1)证明:△DCE≌△FBE;
(2)若EC=3,求AD的长.
如图,已知二次函数y=-x2+bx+c的图象经过A(-2,-1),B(0,7)两点.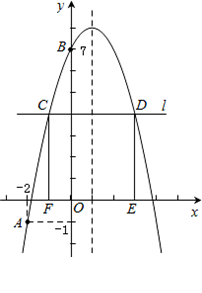
(1)求该抛物线的解析式及对称轴;
(2)当x为何值时,y>0?
(3)在x轴上方作平行于x轴的直线l,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作x轴的垂线,垂足分别为F,E.当矩形CDEF为正方形时,求C点的坐标.
如图1,抛物线 经过(4,0),
经过(4,0),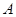
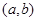 是抛物线上的任意一点,直线
是抛物线上的任意一点,直线 经过
经过 且与
且与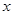 轴平行,过
轴平行,过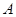 作
作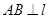 于
于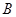 点.
点.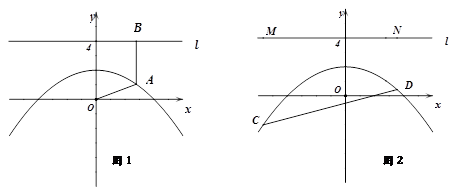
(1)直接写出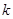 的值:
的值: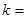 ;
;
(2)当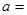 0时,
0时, ,
,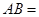 ;
;
当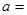 8时,
8时, ,
,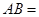 ;
;
(3)由(2)的结论,请你猜想:对于抛物线上的任意一点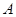 ,
, 与
与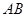 有怎样的大小关系,并证明你的猜想.
有怎样的大小关系,并证明你的猜想.
(4) 如图2,已知线段 12,线段的两端点
12,线段的两端点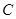 、
、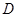 在抛物线上滑动,求
在抛物线上滑动,求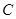 、
、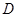 两点到直线
两点到直线 的距离之和的最小值.
的距离之和的最小值.
如图,矩形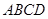 中,
中, ,
, ,点
,点 为
为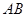 边上一点,
边上一点,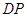 交
交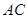 于点
于点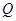 .
.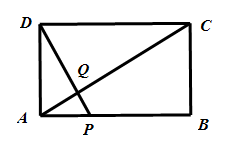
(1)求证: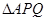 ∽
∽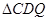 ;
;
(2)当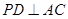 时,求线段
时,求线段 的长度.
的长度.
一只不透明的箱子里共有3个球,把它们的分别编号为1,2,3,这些球除编号不同外其余都相同.
(1)从箱子中随机摸出一个球,求摸出的球是编号为1的球的概率;
(2)从箱子中随机摸出一个球,记录下编号后将它放回箱子,搅匀后再摸出一个球并记录下编号,请用列表或画树状图的方法求两次摸出的球都是编号为3的球的概率.
如图,△ABC在坐标平面内三个顶点的坐标分别为A(1,2)、B(3,3)、
C(3,1).
(1)根据题意,请你在图中画出△ABC;
(2)在原图中,以B为位似中心,画出△A′BC′使它与△ABC位似且位似比是3:1,并写出顶点A′和C′的坐标.